DeepSeek发布了DeepSeek-Prover-V2,这是一个新的开源大型语言模型,专门用于Lean 4中的形式化定理证明。这个模型构建在该公司的DeepSeek-V3基础模型支撑的递归定理证明流水线之上。Lean 4 是微软研究院开发的交互式定理证明助手 Lean theorem prover 的最新版本。这种函数式编程语言和交互式的定理证明系统允许数学家和计算机科学家编写经过机器检查验证的形式化证明。
该项目利用通用 LLM 的能力来处理形式化定理证明的结构化领域的问题,向连接形式化和非形式化数学推理迈出了一步。据研究人员称,他们的方法将复杂的定理分解成更易于管理的组件,从而反映了人类的证明构建方法。
DeepSeek 研究团队扩展了他们的评估框架,专门为形式化定理证明评估设计了新的基准集。
研究人员解释说:“除了标准基准,我们还引入了ProverBench,这是一个包含 325 个形式化问题的集合,其中包括从最近的美国数学邀请赛(American Invitational Mathematics Examination,AIME)竞赛(第 24-25 届)中选出的 15 个问题,以丰富我们的评估内容”。
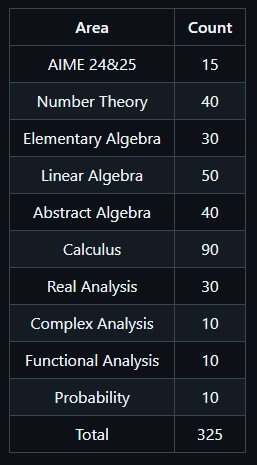
图 1 | 来源:ProverBench - AIME 和教科书问题的形式化
对这些 AIME 问题的初步测试结果表明,他们的专门定理证明模型性能很好。研究小组报告说,DeepSeek-Prover-V2 成功解决了 15 个 AIME 问题中的 6 个,而通用 DeepSeek-V3 模型在使用多数投票技术时则解决了 8 个。
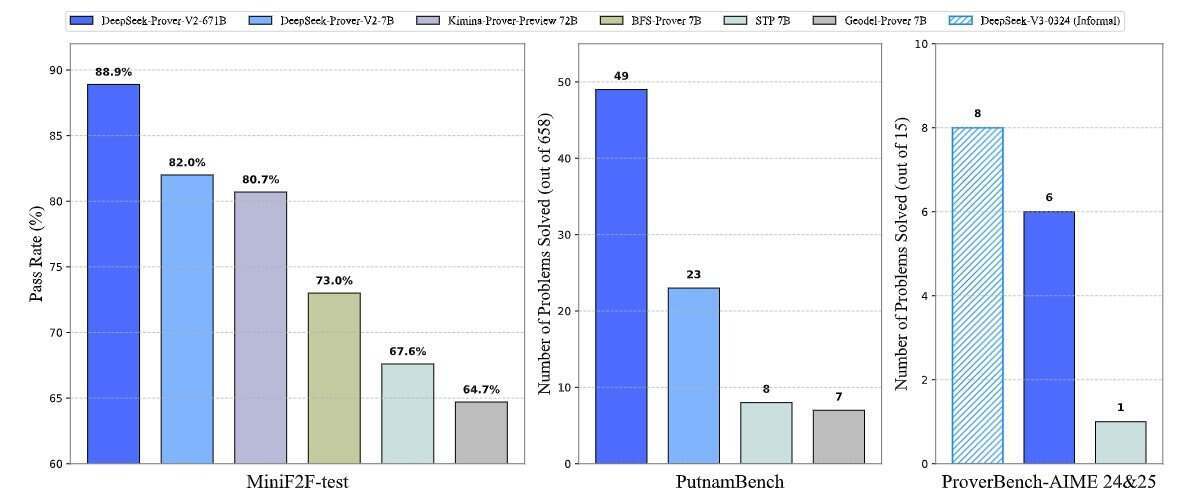
图 2 | 来源:DeepSeek-Prover-V2 的基准性能

图 3 | 来源:将子目标分解为一系列 Lemma 语句
该团队介绍说,“众所周知,通用模型很难生成完整的Lean证明,因为我们会指示 DeepSeek-V3 只生成高级别的证明草图,忽略掉具体的细节。由此生成的思维链最终形成一个 Lean 定理,它由一系列的 have 语句组成,每个语句均以 sorry 占位符结尾,表示有待解决的子目标。这种方式模仿了人类构建证明的方式,也就是将复杂的定理逐步转化为一系列更易于处理的引理。”
然后,系统会采用一种有条理的策略,逐一解决证明的每一个组成部分,从而创造出一种结构化的定理证明方法,这种方法建立在先前已取得的结果基础之上。
研究人员详细介绍说:“利用 DeepSeek-V3 生成的子目标,我们采用递归求解策略来系统性地解决每个中间证明步骤。我们从 have 语句中提取子目标表达式,用它们来替代给定问题中的原始目标(参见图 3(a)),然后将前面的子目标作为前提(参见图 3(b))。这种构造方式使后续的子目标可以利用前面步骤的中间结果来解决,从而促进了更局部化的依赖结构,并有利于开发更简单的引理”。
为了优化计算资源,该系统采用了一个较小的专用 7B 参数模型来处理分解的引理,这有助于管理大量证明搜索的计算需求。当所有分解步骤都成功解决后,该方法最终会自动推导出完整的证明。
研究人员介绍说,“该算法框架分两个阶段运行,利用了两个互补的模型:DeepSeek-V3用于引理分解,7B 证明模型用于完成相应的形式化证明细节。”
这种架构为合成形式化推理数据建立了一个自然的途径,能够有效地将高级数学推理与严格的形式化验证要求融合在一起。
据研究人员介绍,“我们整理了一组 7B 证明模型无法端到端解决的具有挑战性的问题子集,但它们分解后的子目标都已成功解决。通过组合所有子目标的证明,我们为原始问题构建了一个完整的形式化证明”。
尽管在技术上取得了不错的成就,但一些专家还是对实现细节表示了担忧。Epoch AI 公司的首席数学家Elliot Glazer指出了这项研究的潜在问题:
对 DeepSeek-Prover-V2 的论文有一些担忧。Lean zulip 上的讨论表明,PutnamBench的证明是不合理的,并且使用了隐含的 sorry(可能隐藏在 apply?中),并没有在 read-eval-print-loop 中报道。
这些问题凸显了形式化验证领域正在面临的挑战,因为精确的实现细节会对结果的有效性产生重大影响。
DeepSeek 发布了两种不同规模模型的 Prover-V2,分别是基于之前 Prover-V1.5-Base 的7B参数版本,它具有高达 32K 标记的扩展上下文长度,以及基于 DeepSeek-V3-Base 的更大671B参数版本。这两个模型现在都可以在HuggingFace上找到,同时还有包含 325 个形式化问题的完整ProverBench数据集,这主要用于进行评估。对形式化定理证明感兴趣的研究人员和开发人员可以访问这些资源,探索这项技术的能力和局限性,并为解决该领域的专家所提出的问题做出贡献。
查看英文原文:DeepSeek Launches Prover-V2 Open-Source LLM for Formal Math Proofs





