
随着人工智能近十年来的飞速发展,机器学习、深度学习已从学术研究逐步落实到工业界,特别是近几年机器学习框架,如 TensorFlow、Pytorch、CNTK、Keras 等层出不穷,框架设计越来越面向开发者,特别是 TensorFlow.js 的发布、V8 引擎更高性能新版本的发布等等信息,这些好像在告诉我,将深度学习广泛应用到端已然不远了。
为了不被类似 Alpha 狗等 AI 打败,作为一名程序开发者,学习和了解一些机器学习的知识、最新动态信息还是有必要的,而深度学习作为机器学习的一部分,在工业界已经发挥了重要的作用,所以今天就由浅入深,从理论知识到实战编程,逐步探究人工神经网络为何物。
阅读提示
以下内容面向深度学习初学者,需要具备以下基本素质:
①有任何编程语言的编程经验
②对几何代数相关数学知识有基本理解
③对 TensorFlow、Keras 有所了解(不了解也不会有太大影响)
④对 Jupyter Notebook 有所了解(不了解也不会有太大影响)
内容纲要
以下内容分为四个章节,可能需要 30 分钟阅读时间
第一章节——介绍神经网络重要概念和数学推导
第二章节——实战编写逻辑回归模型
第三章节——使用 TensorFlow 实现浅层神经网络
第四章节——使用 Keras 实现深度神经网络
实战编程内容均通过 Jupyter Notebook 承载。
第一章理清神经网络的基础以及实现步骤
感知机
感知器(英语:Perceptron)是 Frank Rosenblatt 在 1957 年就职于康奈尔航空实验室(Cornell Aeronautical Laboratory)时所发明的一种人工神经网络。它可以被视为一种最简单形式的前馈神经网络,是一种二元线性分类器。
Frank Rosenblatt 给出了相应的感知机学习算法,常用的有感知机学习、最小二乘法和梯度下降法。譬如,感知机利用梯度下降法对损失函数进行极小化,求出可将训练数据进行线性划分的分离超平面,从而求得感知机模型。
**生物学-神经细胞**
(神经细胞结构示意图)
**人工神经元**
(神经元结构示意图)
在人工神经网络领域中,感知机也被指为单层的人工神经网络,以区别于较复杂的多层感知机(Multilayer Perceptron)。作为一种线性分类器,(单层)感知机可说是最简单的前向人工神经网络形式。尽管结构简单,感知机能够学习并解决相当复杂的问题。感知机主要的本质缺陷是它不能处理线性不可分问题。
(注:以上内容摘自维基百科)
单层感知机的适用和缺陷
适合解决线性问题,如下图
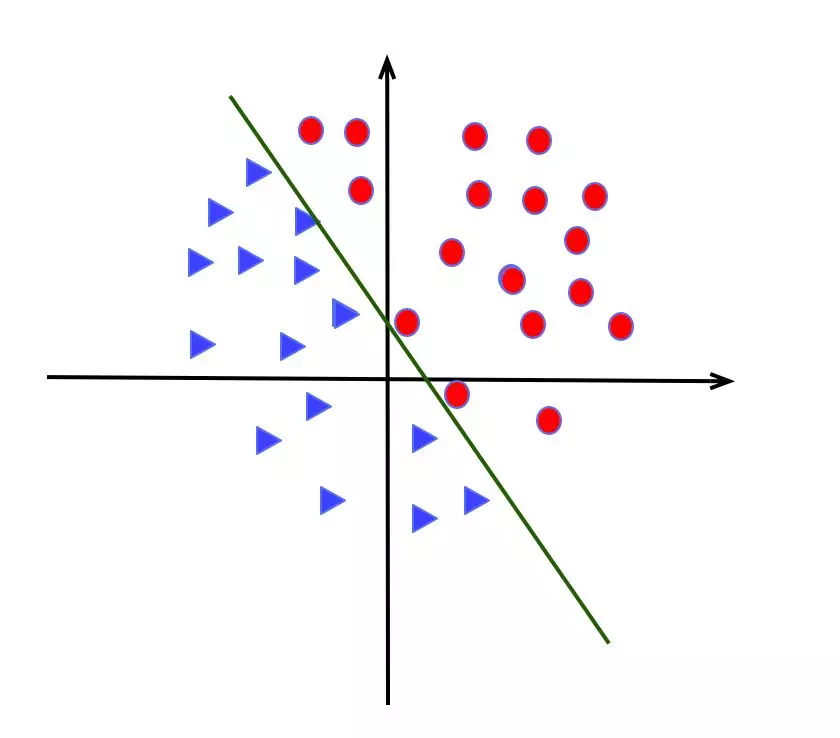
无法解决线性不可分,如常见的 XOR 异或问题,如下图
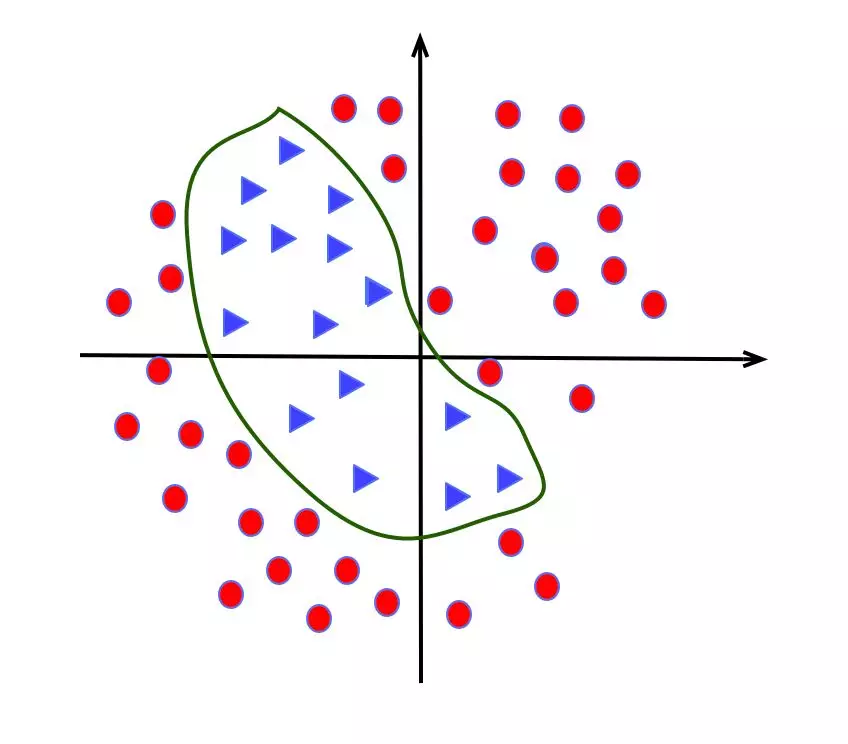
二分类
目前工业界最能产生价值的是机器学习中的监督学习, 场景有推荐系统,反欺诈系统等等。其中二分类算法应用的尤其之多。

例如上面的图像识别场景, 我们希望判断图片中是否有猫,于是我们为模型输入一张图片,得出一个预测值 y。 y 的取值为 1 或者 0. 0 代表是,1 代表否。
逻辑回归模型
逻辑回归是一个用于二分类(binary classification)的算法。
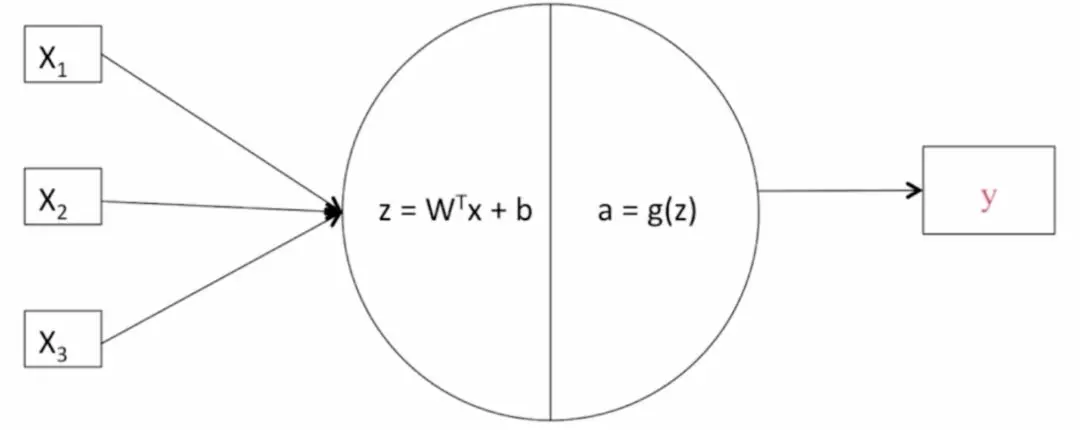
逻辑回归的 Hypothesis Function(假设函数)

sigmoid 函数

逻辑回归的输出函数

激活函数
也叫激励函数,是为了能够给神经网络加入一些非线性因素,使得神经网络可以更好地解决较为复杂的问题。
常见的激活函数
Sigmoid 函数
tanh 函数
ReLU 函数
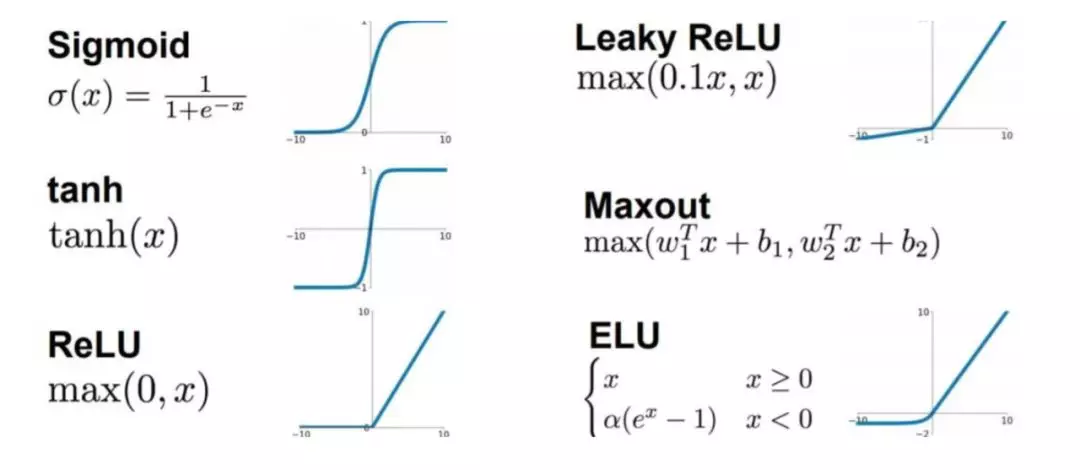
损失函数(Lost Function)

代价函数(Cost Function)
为了训练逻辑回归模型的参数参数𝑤和参数𝑏,我们需要一个代价函数,通过训练代价函数来得到参数𝑤和参数𝑏。
代价函数也叫做成本函数,也有人称其为全部损失函数。
损失函数是在单个训练样本中定义的,它衡量的是算法在单个训练样本中表现如何,为了衡量算法在全部训练样本上的表现如何,我们需要定义一个算法的代价函数。
算法的代价函数是对个 m 样本的损失函数求和,然后除以 m:
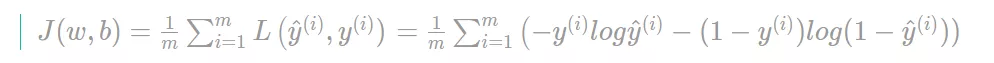
损失函数只适用于像这样的单个训练样本,而代价函数是参数的总代价,所以在训练逻辑回归模型时候,我们需要找到合适的和,来让代价函数 的总代价降到最低。
代价函数的解释

由上述推论可得出这两个条件概率公式:
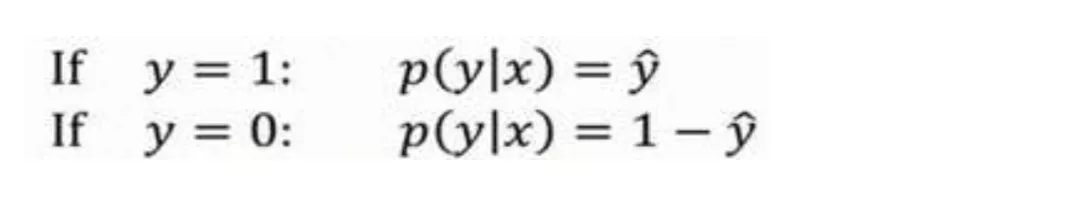
以下类似手写截图均来自吴恩达老师的深度学习课程
可将上述公式,合并成如下公式:
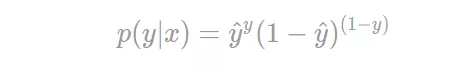
解释合并过程


推导到 m 个训练样本的整体训练的代价函数

计算图
计算图是什么
一个神经网络的计算,都是按照前向或反向传播过程组织的。
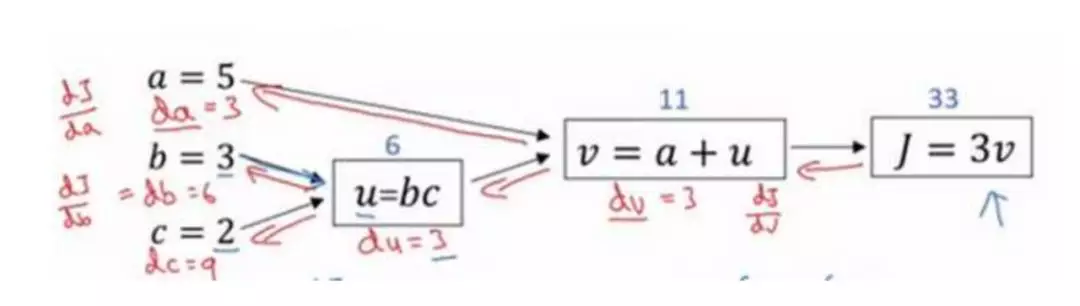
首先我们计算出一个新的网络的输出(前向过程),紧接着进行一个反向传输操作。后者我们用来计算出对应的梯度或导数。
计算图解释了为什么我们用这种方式组织这些计算过程。
举例说明

概括一下:计算图组织计算的形式是用蓝色箭头从左到右的计算
使用计算图求导数
进行反向红色箭头(也就是从右到左)的导数计算
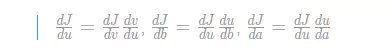
在反向传播算法中的术语,我们看到,如果你想计算最后输出变量的导数,使用你最关心的变量对𝑣的导数,那么我们就做完了一步反向传播。
当计算所有这些导数时,最有效率的办法是从右到左计算,跟着这个红色箭头走。
所以这个计算流程图,就是正向或者说从左到右的计算来计算成本函数 J(你可能需要优化的函数)。然后反向从右到左是计算导数。
梯度下降
梯度下降法 (Gradient Descent)
梯度下降法可以做什么?
在你测试集上,通过最小化代价函数(成本函数)𝐽(𝑤, 𝑏)来训练的参数𝑤和𝑏
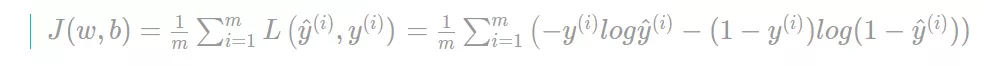
梯度下降法的形象化说明
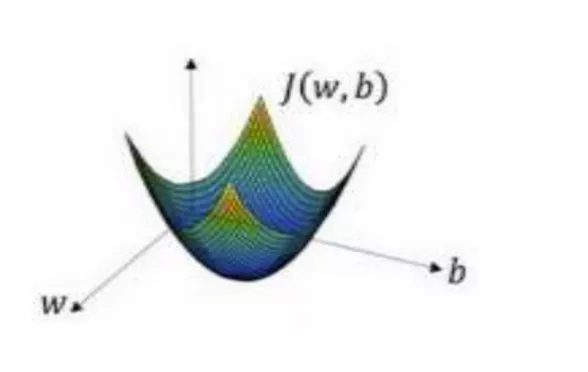
在这个图中,横轴表示你的空间参数𝑤和𝑏,在实践中,𝑤可以是更高的维度,但是为了 更好地绘图,我们定义𝑤和𝑏,都是单一实数,代价函数(成本函数)𝐽(𝑤, 𝑏)是在水平轴𝑤和 𝑏上的曲面,因此曲面的高度就是𝐽(𝑤, 𝑏)在某一点的函数值。我们所做的就是找到使得代价 函数(成本函数)𝐽(𝑤, 𝑏)函数值是最小值,对应的参数𝑤和𝑏。
以如图的小红点的坐标来初始化参数𝑤和𝑏。
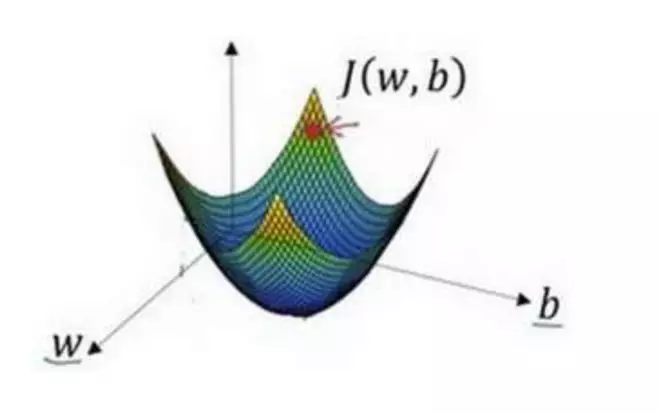
选出最陡的下坡方向,并走一步,且不断地迭代下去。
朝最陡的下坡方向走一步,如图,走到了如图中第二个小红点处。
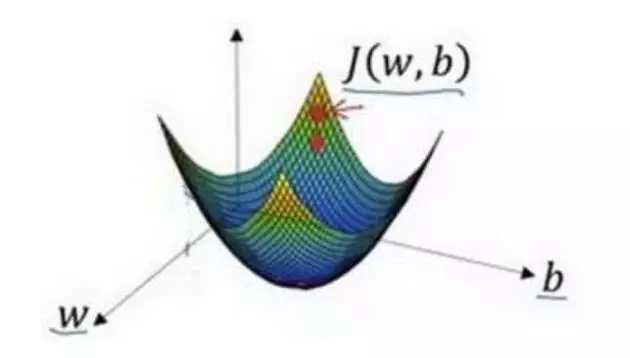
可能停在这里也有可能继续朝最陡的下坡方向再走一步,如图,经过两次迭代走到 第三个小红点处。
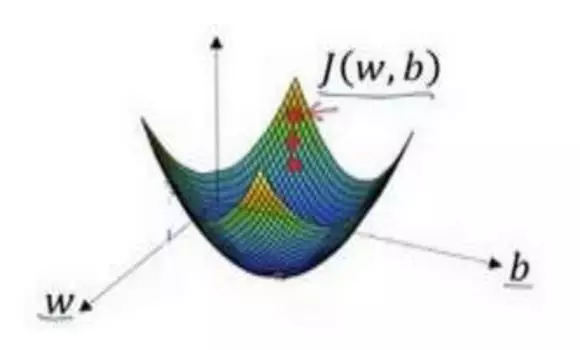
直到走到全局最优解或者接近全局最优解的地方。
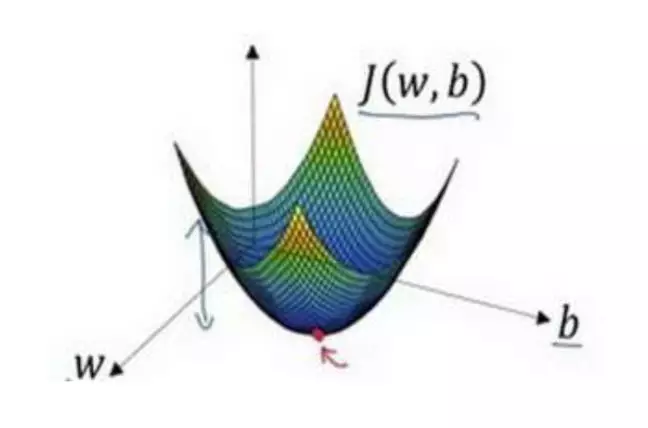
通过以上的三个步骤我们可以找到全局最优解,也就是代价函数(成本函数)𝐽(𝑤, 𝑏)这个凸函数的最小值点。
逻辑回归的梯度下降

反向传播计算 𝑤 和 𝑏 变化对代价函数 𝐿 的影响

单个样本的梯度下降算法

网络向量化
我们已经了解了单个训练样本的损失函数,当使用编程进行计算多个训练样本的代价函数时,一般都会想到使用 loop 循环来计算。
但是在数学科学领域,训练一个模型可能需要非常大量的训练样本, 即大数据集,使用 loop 循环遍历的方式是十分低效的。
线性代数的知识起到了作用,我们可以通过将循环遍历的样本数据,进行向量化,更直接的、更高效的计算,提高代码速度,减少等待时间,达到我们的期望。
注意:虽然有时写循环(loop)是不可避免的,但是我们可以使用比如 numpy 的内置函数或者其他办法去计算。

神经网络实现步骤
在深度学习中,我们一般都会使用第三方框架,如 TensorFlow, Keras,训练过程对我们来说是不可见的。
上面讲了很多的函数、以及其概念、作用,这些神经网络的”组件“,或者说,”组成部分“,如何串联起来呢?以及为什么一开始就会提到 ”前向传播“ 和 ”后向传播“ 这两个概念?
在一个简单神经网络的实现中,简化分为几步:
1、引入外部包
2、加载数据集
3、定义计算图
4、初始化参数
5、一次迭代的前向传播:执行计算图,一层层计算,直到计算到输出层,得到预估值、准确率、损失函数
6、一次迭代的反向传播:对上次得到损失函数求导,使用优化函数(梯度下降算法)从右向左对神经网络的每一层计算调参,直到计算到第一个隐含层,得到优化更新的参数
7、重复(5)(6)为一个迭代,记录多个迭代的信息,训练完毕的模型的最终损失和准确率。
8、使用(7)中得到的训练过程数据,绘制训练集、测试集关于迭代次数与损失的关系曲线图以及迭代次数与准确率关系的曲线图,进行分析,以调整超参数。
第二章逻辑回归(Logistic Regression)实现猫咪识别器
导入所需的 package
加载数据集 (cat / non-cat)
查阅训练集中的一张图片
一张正确分类的图片

一张错误分类的图片

猫咪图片数据处理过程示意
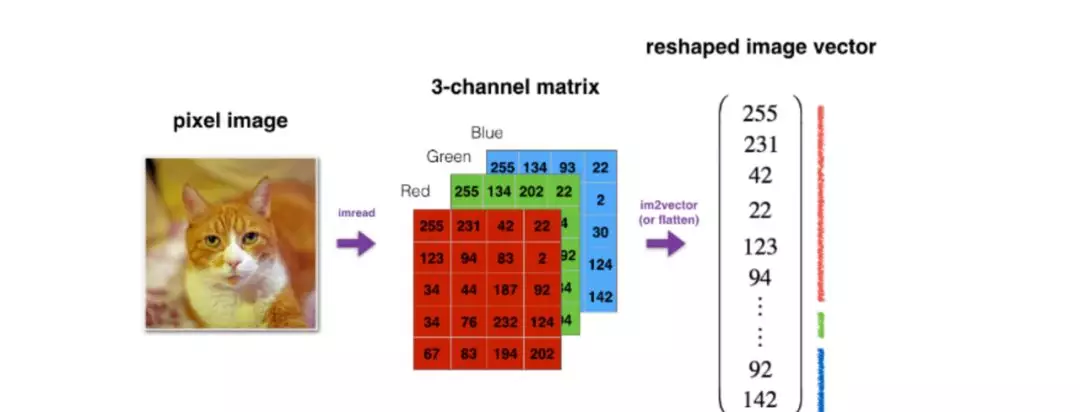
实现输入数据扁平变形和标准化(也叫归一化)
将训练集和测试集中的 x 维度切分为(num_px * num_px * 3, m)的形式
reshape 目的:实现矩阵乘法计算
x 维度切分为(num_px * num_px * 3, m)的形式。
y 维度切分为(1, m)的形式。
标准化目的:预处理的数据被限定在一定的范围内(比如[0,1]或者[-1,1]),从而消除奇异样本数据导致的不良影响。
实现激活函数
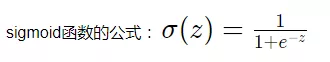
实现初始化参数函数
如图小红点的坐标来初始化参数𝑤和𝑏。

实现代价函数(前向传播)和梯度下降函数(反向传播)
前向传播
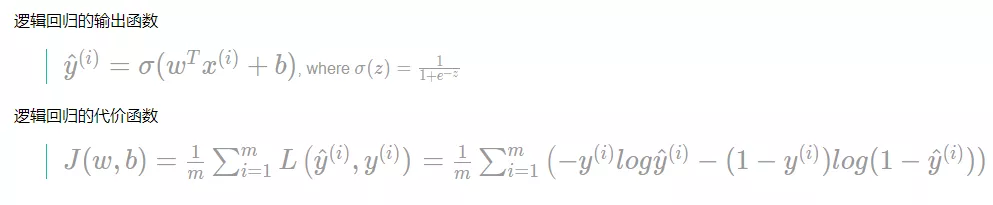
反向传播

实现调参函数
以梯度下降算法不断更新参数,使其达到更优。
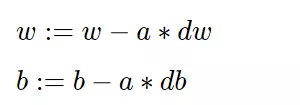











评论