无痛的增强学习入门：差分时序法

系列导读：《无痛的增强学习入门》系列文章旨在为大家介绍增强学习相关的入门知识，为大家后续的深入学习打下基础。其中包括增强学习的基本思想，MDP 框架，几种基本的学习算法介绍，以及一些简单的实际案例。

作为机器学习中十分重要的一支，增强学习在这些年取得了十分令人惊喜的成绩，这也使得越来越多的人加入到学习增强学习的队伍当中。增强学习的知识和内容与经典监督学习、非监督学习相比并不容易，而且可解释的小例子比较少，本系列将向各位读者简单介绍其中的基本知识，并以一个小例子贯穿其中。

• 无痛的增强学习入门：基本概念篇
• 无痛的增强学习入门： 增强学习形式化
• 无痛的增强学习入门：策略迭代
• 无痛的增强学习入门：价值迭代
• 无痛的增强学习入门：泛化迭代
• 无痛的增强学习入门：蒙特卡罗方法

7 差分时序法

7.1 蒙特卡罗的方差问题

上一节我们介绍了蒙特卡罗法，它可以比较好地解决无模型场景下的蛇棋问题。当然，它也存在着一定的不完美，这些不完美体现在很多方面，接下来我们就来看一看其中的一个问题——估计值的方差问题。

前面我们已经知道，蒙特卡罗是用一系列的模拟游戏得到一些 episode 的回报信息，然后用这些回报信息求平均，就可以得到估计的价值函数。这个方法从理论上讲是没有问题的，它能够成立的根本在于概率论中的大数定理。大数定理也是没有问题的，可是大数定理只说明了收敛性，并没有说明收敛的速度。很显然，如果采样序列的方差比较大，那么想要让它收敛就需要更长的时间，如果采样序列的方差较小，那么收敛的速度也会相应地降低。

基于上面的分析，我们就来看看前面的蒙特卡罗法存不存在方差方面的问题。我们用上一节的方法进行计算，同时保存 state=50,action=1 的 return 值，将所有的值综合起来做成一个直方图，如图 7-1 所示。

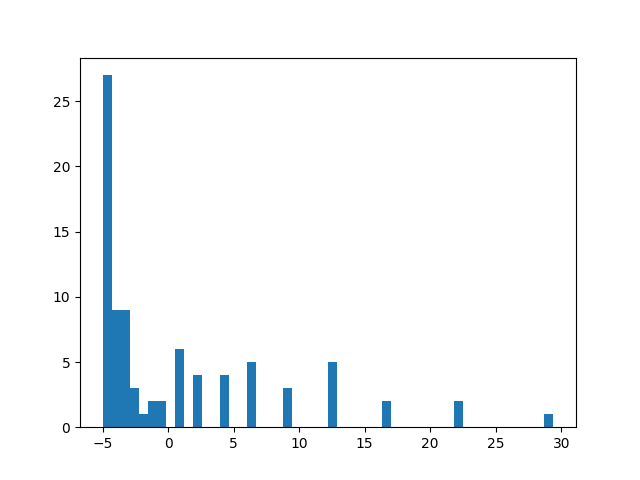
图 7-1 蒙特卡罗法 every-visit 的 return 收集直方图

可以看出，return 的跨度还是比较大，这样模型就不太容易收敛。

当然，跨度大和其他问题也有关系，其中一个关系就是 episode 中的采样频率。上一节采用的方法叫做"every-viist"，也就是说 episode 中的每一个 state-action 对都会参与到计算当中，这样就为统计带来了困难。因为在蛇棋这个游戏中，由于有梯子的存在，某一个位置可能被走过两次。比方说例子中的位置“50”，我们在计算的过程中没有区分第一次到达“50”和第二次到达“50”，而且将这两个 return 直接加在了一起，由于这两次的 return 一定有差异，因此这样的统计方式会让方差增大，从而难以收敛。

那么该如何应对这个问题呢？一个解决方案是把"every-visit"方法换掉，改成"first-visit"法。所谓的"first-visit"法就是只统计第一次出现的状态，对于后面出现的同一状态则不再统计。从方法的理念来说，同一个 episode 内因多次出现同一状态而造成方差增大的问题将得到解决。下面就来看看"first-visit"的结果：

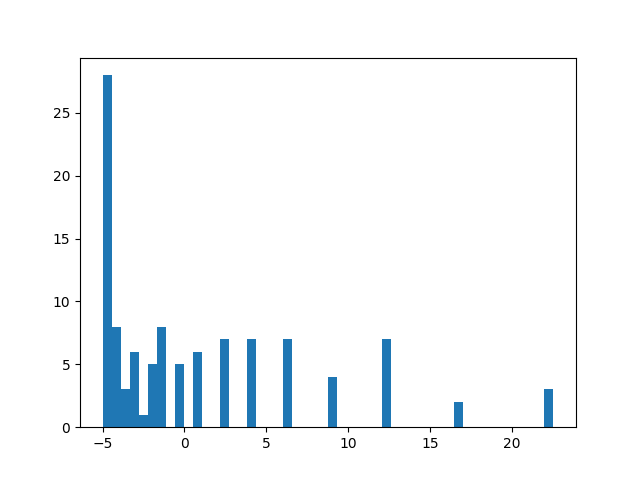
图 7-2 蒙特卡罗法 first-visit 的 return 收集直方图

从结果来看，first-visit 的效果稍有提高，但是并没有明显的提高。因为即使只取一个不重复的状态，我们仍然会遇到不同情况的 first-visit，每种之间的数值差距依旧很大。

既然蒙特卡罗法存在着这样一些遗憾，那么我们就来看看接下来介绍的方法：差分时序法（Temporal Difference）。

7.2 差分时序

差分时序法是一种结合了蒙特卡罗法和动态规划法的方法。从算法的主体结构来看，它同蒙特卡罗法类似，同样通过模拟 episode 的方式进行求解；从算法的核心思想来说，它有用到了增强学习中的经典公式——Bellman 公式进行自迭代更新。

前面提到状态 - 行动价值函数的 Bellman 公式的形式为：

\(q(s,a)=\sum_{s’}p(s’|s,a)[R + \sum_{a’} \pi(a|s’)q(s’,a’)]\)

那么利用蒙特卡罗的方法，我们就可以将公式变为：

\(q(s,a)=\frac{1}{N} \sum_{i=1}^N [R(s’_i)+q(s’_i,a’_i)]\)

当然，这个公式还可以变成前面蒙特卡罗法中实际应用的形式：

\(q_t(s,a)=q_{t-1}(s,a)+\frac{1}{N}[R(s’)+q(s’,a’)-q_{t-1}(s,a)]\)

从这个公式我们可以看出这个方法和蒙特卡罗、动态规划的关系来。下面我们就来实现这个方法，我们首先要实现的方法被称为"SARSA"，这个名字看上去有些奇怪，其实它来自于这个方法的五个关键因子：S(待求状态)，A(待求行动)，R(模拟得到的奖励)，S(模拟进入的下一个状态)，A(模拟中采取的下一个行动)。

7.3 On-policy：SARSA

接下来就来实现这个算法，其实它的实现过程也比较简单，这里只展现评估的过程：

for i in range(episode_num):
env.start()
state = env.pos
prev_act = -1
while True:
act = self.policy_act(state)
reward, state = env.action(act)
if prev_act != -1:
return_val = reward + (0 if state == -1 else self.value_q[state][act])
self.value_n[prev_state][prev_act] += 1
self.value_q[prev_state][prev_act] += (return_val - \
self.value_q[prev_state][prev_act]) / \
self.value_n[prev_state][prev_act]
{1}
prev_act = act
prev_state = state
{1}
if state == -1:
break
{1}

那么这个代码的实现效果如何呢？我们同样写一段测试的代码。

def td_demo():
np.random.seed(0)
env = Snake(10, [3,6])
agent = MonteCarloAgent(100, 2, env)
with timer('Timer Temporal Difference Iter'):
agent.td_opt()
print 'return_pi={}'.format(eval(env,agent))
print agent.policy
 
agent2 = TableAgent(env.state_transition_table(), env.reward_table())
with timer('Timer PolicyIter'):
agent2.policy_iteration()
print 'return_pi={}'.format(eval(env,agent2))
print agent2.policy

为了试验效果，我们将 SARSA 算法中的迭代轮数增加到 2000，最终的结果为：

Timer Temporal Difference Iter COST:3.8632440567
return_pi=80
[0 0 0 1 1 1 1 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0]
policy evaluation proceed 94 iters.
policy evaluation proceed 62 iters.
policy evaluation proceed 46 iters.
Iter 3 rounds converge
Timer PolicyIter COST:0.330899000168
return_pi=84
[0 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0]

从结果可以看出，SARSA 算法的效果并不够好，当然我们还没有加入更多的策略来提升效果。不过看上去它的结果还不及蒙特卡罗，那么它和蒙特卡罗相比有什么优势呢？我们来看看前面提到的方差问题，再来看一看 SARSA 算法的结果图：

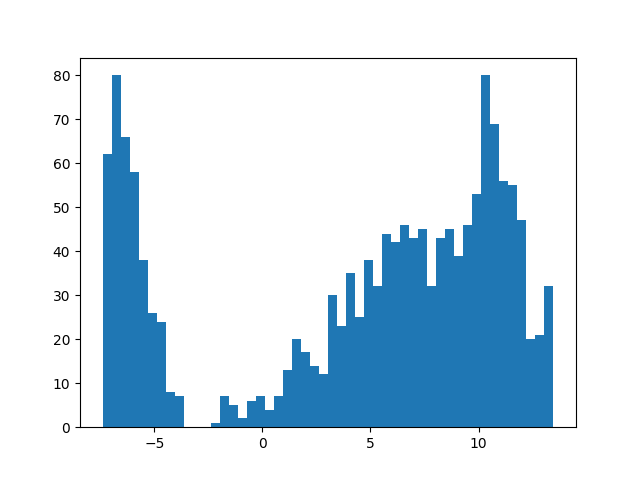
图 7-3 TD 法的 return 收集直方图

可以看出，这个方法的数值变动和前面相比要更为稳定一些，跨度比之前要小一些。

那么为什么 TD 系列的方法会在方差方面控制得更好一些呢？答案就在它的更新公式上。蒙特卡罗的计算方法由于使用了精确的 return，所以在对价值的估计上更精确一些，但是同时它要一个序列的信息，而序列的信息存在更多的波动，所以方差会比较大；而 TD 方法只考虑了一步的计算，其余的计算均使用了之前的估计，所以当整体系统没有达到最优时，这样的估计都是存在偏差的，但是由于它只估计了一步，所以它在估计值方面受到的波动比较少，因此带来的方差也会相应减少许多。

所以前人们发现，蒙特卡罗法和 TD 法象征着两个极端——一个为了追求极小的误差而放松了方差，一个为了缩小方差而放松了误差。这个问题仿佛回到了机器学习的经典问题——bias 和 variance 的权衡问题。

那么，除了 SARSA 这一种方法，还有没有别的算法呢？最后一节我们再来看看 TD 的另一种算法。

作者介绍

冯超，毕业于中国科学院大学，猿辅导研究团队视觉研究负责人，小猿搜题拍照搜题负责人之一。2017 年独立撰写《深度学习轻松学：核心算法与视觉实践》一书，以轻松幽默的语言深入详细地介绍了深度学习的基本结构，模型优化和参数设置细节，视觉领域应用等内容。自 2016 年起在知乎开设了自己的专栏：《无痛的机器学习》，发表机器学习与深度学习相关文章，收到了不错的反响，并被多家媒体转载。曾多次参与社区技术分享活动。