本文要点
- 数据流中产生的巨量数据使流处理查询不可能计算出精确的答案。
- 近似计算近期倍受瞩目,因为它能够以较低的资源占用“针对目标”得出适合的结果。
- 数据流处理应用可以使用近似计算算法或数据结构(比如 HyperLogLog, Count-min Sketch 等等)对结果进行估算。
- 关键是选择适当的近似计算技术操作流处理窗口,以确保可靠的系统运转。
- 现有大多数高数据速率流都可以通过使用近似计算获益。
1. 简介
近期,由于流处理应用需求的不断增长,数据流处理已经成为用于数据分析的主要范式之一。最近几个不同的流处理应用可用于广泛的领域,比如 电信、车辆交通管理、人群管理、健康信息、网络安全、财务等。
巨量的流数据给处理这种数据洪流带来了挑战。针对此问题多种解决方案应运而生,比如升级系统硬件、通过弹性扩展将额外的资源提供到外部云中,随机丢失事件、近似计算,等等。其中的近似计算与其他的方法相比,因为它不需要提供额外的资源而成为了更有希望的方法。
由于几个原因,使近似计算变得更加重要。首先,近似的输出结果可以充分满足许多用例。特别是当趋势数据比精确数据更重要的时候。举个例子,了解访问了一个类似于“易贝”的网站的客户数量,这个数量达到了几亿的级别。通常,你不需要精确了解上一小时访问你网站的客户数。计算精确的数字需要几分钟的时间。而了解大概的数字只需要一秒钟,显然它更实用。
其次,放宽精确度要求能节省很多资源,比如CPU 处理时间和内存。节省系统资源对实现实用的物联网(IoT)应用极其重要,这些边缘服务器上设备是以低能耗运维的。此外,它使大型数据集检索成为可能。
在本文中,我们讲述了一个API 监控应用的真实案例,它就使用近似流处理得到了好处。我们在 WSO2 Stream Processor 之上开发了这款应用,将其作为 Siddhi 的扩展。Siddhi 是一个复杂事件处理类库,它充当 WSO2 流处理的事件处理引擎。
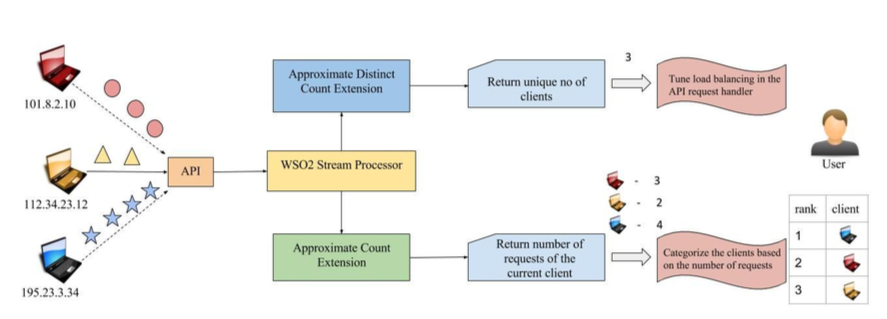
从不同客户端到特定 API 的 HTTP 请求会转到流处理器,以分析独立用户的数量(如图 1 所示)。这个结果用于 API 的负载均衡,可以基于每个客户端的访问数量进行客户端分类。我们使用一系列随机生成的 IP 地址来管理测试。我们定义了如下的输入流:
define stream requestStream(ip String, timestamp long);列表 1: 输入流的定义
图1:监控API 访问统计信息
我们发现无重复计数(Distinct Count)和计数(Count )函数的吞吐量分别有144% 和66% 的提升,而延迟有78% 和45% 的提升。产生的结果有+/- 5% 的误差范围,也就是说结果的精确率在5% 之内。那么,这种处理结果的上下限就可以按如下计算了:
lower bound result = approx result - (approx result * 0.05) upper bound result = approx answer + (approx answer * 0.05)
清单 2:结果的上下限是如何定义的。
这个误差范围以两个配置参数来确定,名叫相对误差(relative error)和信心(confidence)。为了达成 +/- 5% 的误差,得用 0.1 的相对误差和 0.95 的信心。因为我们可以使用 Java 的整形数(它们是 32 位的)来表示哈希,所以我们选择用 +/- 5% 的误差范围。这个 5% 的误差对当于 400 多个桶,每个桶的 ID 是 9 位。这和 32 位的 1/4 很接近。本文所说的近似计算功能已经作为开源软件发布了。
在本文中,我们首先介绍了我们用来实现近似计算的技术(比如,HyperLogLog 和Count-min Sketch)。然后,介绍了我们的实现方式和旨在改善近似算法好处的实验。通过这个结果,我们发现这一做法很有前途,近似计算与“初级做法”相比在交付结果时可以保持更高的吞吐率和更低的延迟。本文在总结部分又特别强调了这些好处。
2. 用于近似计算的技术
最近两个近似计算算法已经用于实现 WSO2 流处理器中的近似计算函数了。它们是 HyperLogLog 和 Count min-sketch 算法,我们将在下面的小节中予以介绍。
2.1 近似的无重复计数:HyperLogLog
HyperLogLog 是一个用于统计集合中条目的近似基数(比如无重复元素的个数)的算法。与其他方法形成对照的是,它以数据概要来跟踪掌握统计的情况,而不是获取数据集中的所有唯一条目。该算法的主要思想是使用特定位组合在一组位串中的重现概率来统计唯一的条目。因此,在更新条目概要之前,这些条目会用哈希函数转换为位串。近期出现了几个 HyperLogLog 的应用,比如蠕虫传播的检测、网络攻击的检测、网络通讯监控,等等。
算法1:HyperLogLog 算法
以上向大家介绍了HyperLogLog 算法(如算法1)。算法的输入是数据条目的多重集V。HyperLogLog 的输出是对基数的评估,即V 中无重复元素的数量。HyperLogLog 算法使用一个固定大小的整形数组来保存数据集的基数(无重复条目的计数)的计数。
HyperLogLog 使用模式重现的思想。我们来想一个场景,b=4,即我们取位串左边的首四位字节。一个 0000xxx…的位串,其出现的概率为 1/16(即 1/(2⁴))。那么 0000 模式就可以代表数据集中 6.25% 的数据。有高的概念在 16 (=2⁴) 个不同的串会出现重复的情况。因此,通过维护插入值的最大位模式,就能够获得非重复值的近似数目。
按 HyperLogLog 进行简单评估会出现偏差。因此,为改进这个算法,通过使用固定大小的前缀并用一种平均技术计算最终的评估,将输入分类到不同的桶(数组单元格)。在下面的示例中,前缀长度为 3 个字节。然后输入的剩余部分用于找出最大的位模式(也就是说,连续的 0)。
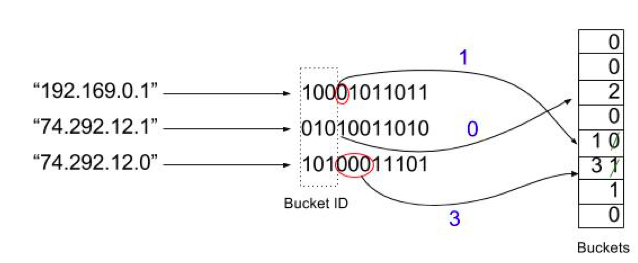
图2:HyperLogLog 函数的示例
下面,要插入数值了。假设有如图2 所示的三个IP 地址。首先,他们会通过一个哈希函数转换为位串。在此,考虑将前3 位作为桶的id。然后把位串剩余部分中连续0 的数目放入到桶中,除非桶里已经有更大的了。
通过计算所有桶中的值的调和平均数,查询的值就出来。
清单1:用于调和平均数的公式
调和平均公式如清单1 所示。调和平均用于正常化结果。
2.2 近似计数:Count-min Sketch
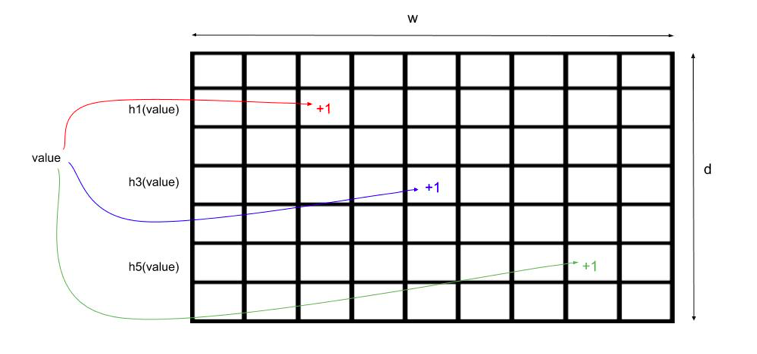
Count-min Sketch 算法使用一个二维数据保存进入特定集合中的值的数目。数组的宽度是 w,高度是 d,表示用到的哈希函数的数目(如图 3 所示)。
图3:Count-min Sketch 使用的二维数组
参数w 和d 由预期的输入精度决定。特别要说的是,w 和d 是可被计算的:
清单2:Count-min Sketch 的二维数据的宽度
e 是自然对数的底数,_ε_ 是相应的误差。
清单3:Count-min Sketch 的二维数据的高度
_δ_ 在这里是对含有特定相对误差的答案的信心。
插入一个值如下所述。假设有 d 个哈希函数(h0、h1……),每个哈希函数映射 0、1…、w-1 中的一个值。假设该哈希值的取值是这样的:h1(值)=2、…、h3(值)=4、…、h5(值)=7…在此,与哈希函数相关的每个单元格里的值都是按 1 递增的。
从二维数组中查询一个值如下所述。假设,你想知道值 x 的数量。那么所有 x 的哈希值都按 h1(x) = 1, h2(x) =3 , …, hd(x) = 2 予以计算。取出这些值的单元格中最小的值作为答案。
Count = min{cell_value(h1(x)), cell_value(h2(x)), …, cell_value(hd(x))}清单 4:Count-min Sketch 的二维数组的高
Count-min Sketch 算法不理解这个值。但由于不同的值会映射到经过哈希的同一单元格中,所以会发生高估。
3. 我们的做法
在本节中,我们讲讲我们是如何实现 HyperLogLog 和 Count-Min-Sketch 算法,将其作为 Siddhi 扩展的。无重复计数和计数扩展都被实现为流处理扩展了。
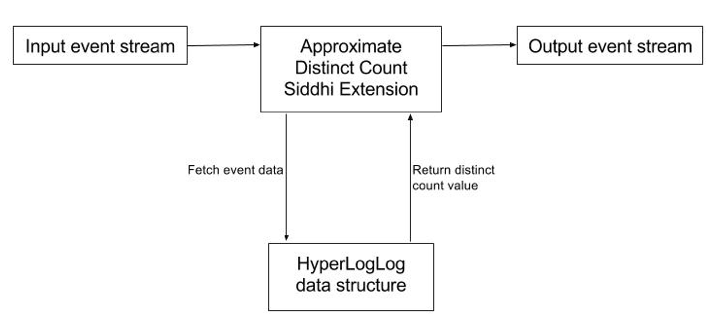
该近似无重复计数扩展(如图 4 所示)处理来自输入流的输入事件,并更新数据概要(HyperLogLog 数据结构)。然后使用概要中保存的数据计算当前的无重复计数的值,最后以输出事件返回。
图4:近似无重复计数Siddhi 扩展的架构
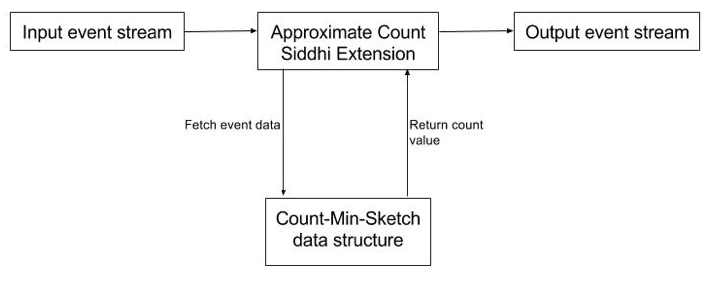
该近似计数扩展(如图5 所示)处理来自输入流的输入事件,并更新数据概要(Count-Min-Sketch 数据结构)。然后使用概要中保存的数据计算当前的唯一计数的值,最后以输出事件返回。
图5:近似计数Siddhi 扩展的架构
不像近似计算的传统应用(比如数据库),如果使用事件窗口时候去利用无重复计数和计数这种近似计数技术,必须要格外地谨慎。这两种技术一般默认会随事件窗口一起运转。然而,如果一个窗口未在无重复计数运算之前使用,那么无重复计数可能消耗过多的系统内存。这是因为,默认情况下,窗口会令无重复计数组件内累积的事件到期。但是,如果一个窗口没被使用过,那么就不会触发这种到期的情况。于是,无重复计数扩展内的事件就会无限累积。
4. 实验
在简介一节中提到的那个示例应用中,我们很想要测量我们的应用程序处理每秒所收到的大量 HTTP 请求的能力。为了模拟以上这种的场景,我们实现了一个生成随机 IP 的客户端应用。我们还实现了另一个应用,它使用 Siddhi 流处理器去处理由客户端发送的事件,计算无重复计数和计数的值。注意,在该数据集内,随机生成的 IP 可能会重复。
针对以下四种不同场景度量输出吞吐量和延迟:
- 使用非近似的(精确)Siddhi 查询去计算事件的无重复计数
- 使用近似 Siddhi 查询去计算事件的无重复计数
- 使用非近似的(精确)Siddhi 查询去计算事件的计数
- 使用近似的 Siddhi 查询去计算事件的计数(频繁)
对比场景 1 和场景 2 的性能结果,以及场景 3 和场景 4 的性能结果。
应用客户端和服务端运行在以以太网电缆连接的机器上,通过 TCP 通道来发送事件。运行应用客户端的计算机(联想 T520 笔记本电脑)的配置是 Intel Core i7-2630M, 2.00GHz, 8 核 和 8GB 内存。运行服务端的计算机(联想 T530 笔记本电脑)的配置是 Intel Core i7-3520M, 2.90GHz, 4 核 和 8GB 内存。这两台计算机都安装了 LinuxUbuntu(16.04 LTS) 64 位版、Siddhi 4.0.0 和 Oracle JDK 1.8。它们分配了最大和最小 JVM 堆为 4GB。
该实验针对近似无重复计数扩展和近似计数扩展的性能度量进行了分类。针对每一类,我们运行一个脚本到 Siddhi 事件流中取事件。为观测初级做法的性能,事件流是通过 Siddhi 查询来传递的,这个查询使用这个初级方法来计数。基于输出事件的查询来计算吞吐量和延迟的值。
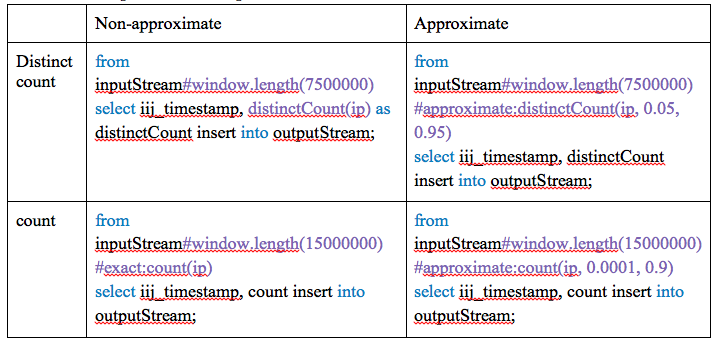
为了度量这个扩展的性能,将 Siddhi 查询改成使用近似扩展,其他所有都保持不变,对吞吐和延迟进行了度量。注意,这个吞吐量和延迟的度量针对的是从 Siddhi 查询每一百万的事件输出。因此,在这些实验中使用的窗口规模为一百万。在本次实验中使用的查询如表 1 所示。
表 1:查询对照
5. 结果
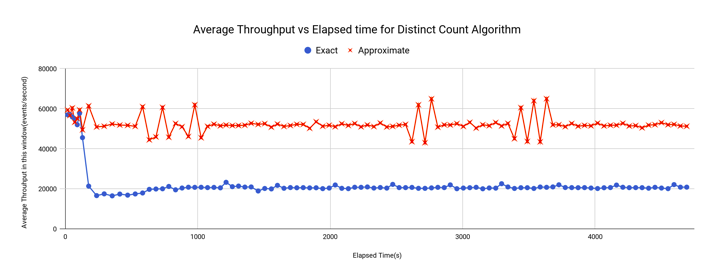
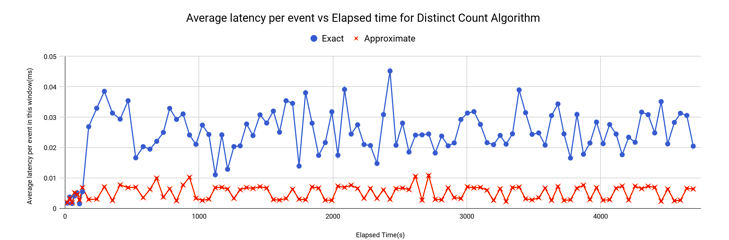
使用非近似的方法去计算事件的无重复计数时,报告的全部吞吐量为每秒大约 21,312 个事件,总体平均延迟每事件约为 0.02424607 毫秒。应当注意的是,输入事件是按非近似法所能处理的最大速率来发送的。这是因为,使用这么高的输入数据率能更清晰地说明用近似计算技术的好处。使用近似无重复计数扩展时,报告的总体吞吐率为每秒约 52,012 个事件,它有 144% 的提升,而总体平均延迟每个事件是大约 0.00522114 毫秒,这有 78% 的改进。无重复计数的平均吞吐量和平均延迟的变化如图 6 和图 7 所示。你可以发现,吞吐量和延迟曲线开始时差不多,非近似算法的性能下降很快,而近似版本从一开始到实验结束都保持同样的性能。
图6: 无重复计数查询的平均吞吐量变化
图7: 无重复计数查询的平均延迟变化
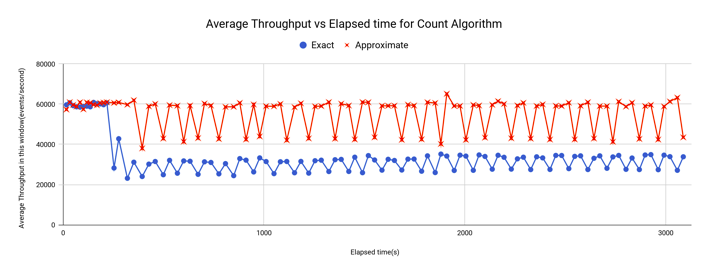
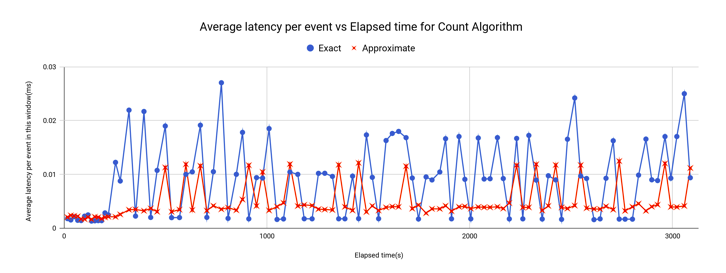
使用非近似法计算(频繁)事件计数时,报告的总体吞吐量为每秒约32,390 个事件,总体平均延迟每事件约为0.0087243 毫秒。使用近似计数扩展时,报告的总体吞吐量每秒约54,070 个事件,它有66% 的提升,总体平均延迟为每事件约0.00475573 毫秒,这有45% 的提升。计数查询的平均吞吐量和平均延迟的变化如图8 和图9 所示。从性能曲线可以看出,计数查询和无重复计数查询的性能表现类似。
图8:计数查询的平均吞吐量变化
图9:计数查询的平均延迟变化
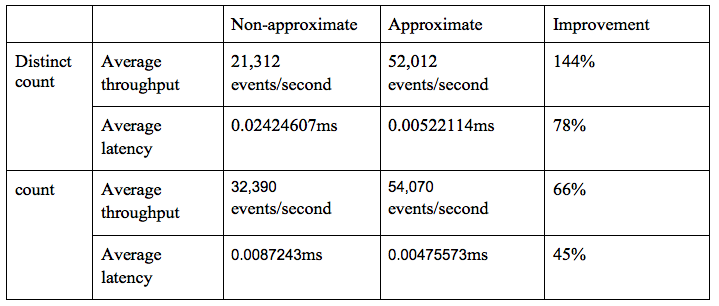
以上图表的总体结果汇总为表2。
表2:实验结果汇总
6. 总结
越来越多的近似计算成为数据流管理的主流技术,它可以比精确的处理方式更有效率地使用系统资源。在本文中,我们介绍了一个已经成功应用于 API 监控应用的近似计算技术的例子。结果表明,与初级做法相比,近似计算完全有希望在保持高吞吐率和低延迟的情况下交付结果。我们还指出,应认识到近似流管理扩展的设计的重要性,应小心仔细,使它们可以可靠地运转。无重复计数和计数扩展已经作为 WSO2 Siddhi 扩展开发完成。在 Apache 2.0 开源许可下可以使用这些扩展。
关于作者
 Chamod Samarajeewa WSO2 的一名实习软件工程师。他目前在斯里兰卡的莫勒图沃大家读计算机科学与工程专业的第三年本科。他的研究兴趣包括数据流处理和近似计算。
Chamod Samarajeewa WSO2 的一名实习软件工程师。他目前在斯里兰卡的莫勒图沃大家读计算机科学与工程专业的第三年本科。他的研究兴趣包括数据流处理和近似计算。
 Miyuru Dayarathna 是 WSO2 的一名高级技术负责人。他是一个有着广泛研究兴趣的计算机科学家,在流式计算、图像数据管理和挖掘、云计算、性能工程及物联网等领域都有贡献。他还是斯里兰卡的莫勒图沃大家读计算机科学与工程专业顾问。他还在驰名的国际期刊上发表过论文,组织过几次高性能图像数据管理与处理的研讨会。
Miyuru Dayarathna 是 WSO2 的一名高级技术负责人。他是一个有着广泛研究兴趣的计算机科学家,在流式计算、图像数据管理和挖掘、云计算、性能工程及物联网等领域都有贡献。他还是斯里兰卡的莫勒图沃大家读计算机科学与工程专业顾问。他还在驰名的国际期刊上发表过论文,组织过几次高性能图像数据管理与处理的研讨会。
查看英文原文: Approximate Computing on WSO2: Explaining Approximation Algorithms in an Applied Setting


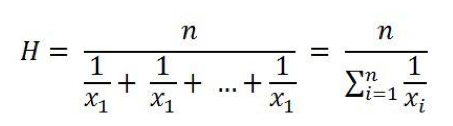
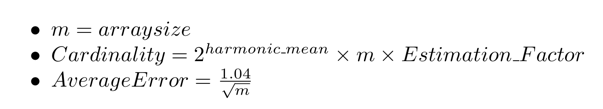









评论