一起学习朴素贝叶斯

最近小编也在开始学习一些机器学习方面的知识。所以就从朴素贝叶斯入手，给大家整理了一下相关的信息，供大家参考学习。

简介

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法，对于给定的训练数据集，首先基于特征条件独立假设学习输入 / 输出的联合概率分布；然后基于此模型。对于给定的输入 x, 利用贝叶斯定理求出后验概率最大的输出 y, 朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。

人物介绍

贝叶斯，英国数学家.1701 年出生于伦敦，做过神甫.1742 年成为英国皇家学会会员.1763 年 4 月 7 日逝世. 贝叶斯在数学方面主要研究概率论. 他首先将归纳推理法用于概率论基础理论，并创立了贝叶斯统计理论，对于统计决策函数、统计推断、统计的估算等做出了贡献.1763 年发表了这方面的论著，对于现代概率论和数理统计都有很重要的作用. 贝叶斯的另一著作《机会的学说概论》发表于 1758 年. 贝叶斯所采用的许多术语被沿用至今。 他对统计推理的主要贡献是使用了 " 逆概率 " 这个概念，并把它作为一种普遍的推理方法提出来。贝叶斯定理原本是概率论中的一个定理，这一定理可用一个数学公式来表达，这个公式就是著名的贝叶斯公式。 – 摘自 360 百科

算法原理

• 条件概率公式
• 全概率公式
• 特征条件独立假设

1 条件概率公式

条件概率是指事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为：P(A|B)，读作“在 B 条件下 A 的概率”。若只有两个事件 A，B，那么：

P(A|B) = P(AB)/P(B)
P(B|A) = P(AB)/P(A)
所以：
P(A|B) = P(B|A) * P(A) / P(B)

2 全概率公式

如果事件 A1、A2、A3…An 构成一个完备事件组，即它们两两互不相容，其和为全集；并且 P(Ai) 大于 0，则对任一事件 B 有：

P(B) = P(A1B) + P(A1B) + ··· + P(AnB)
     = ∑P(AiB)
     = ∑P(B|Ai) * P(Ai) ·······················（i=1，2，····，n）

3 贝叶斯公式

将全概率公式带入到条件概率公式当中，对于事件 Ak 和事件 B 有：

P(Ak|B) = [ P(Ak) * P(B|Ak) ] / ∑P(B|Ai) * P(Ai） ·········（i=1，2，····，n）

对于 P(Ak|B) 来说，分子 ∑P(B|Ai)*P(Ai) 为一个固定值，因为我们只需要比较 P(Ak|B) 的大小，所以可以将分母固定值去掉，并不会影响结果。因此，可以得到下面公式：

P(Ak|B) = P(Ak) * P(B|Ak)

P(Ak) 先验概率，P(Ak|B) 后验概率，P(B|Ak) 似然函数

4 特征条件独立假设

在分类问题中，常常需要把一个事物分到某个类别中。一个事物又有许多属性，即 x=(x1,x2,···,xn)。常常类别也是多个，即 y=(y1,y2,···,yk)。P(y1|x),P(y2|x),…,P(yk|x)，表示 x 属于某个分类的概率，那么，我们需要找出其中最大的那个概率 P(yk|x)。

根据上一步得到的公式可得：P(yk|x) =P(yk) * P(x|yk)
样本 x 有 n 个属性：x=(x1,x2,···,xn)，所以：P(yk|X) =P(yk) * P(x1,x2,···,xn|yk)
条件独立假设，就是各条件之间互不影响，所以：P(x1,x2,···,xn|yk) = ∏P(xi|yk) 最终公式为：P(yk|x) =P(yk) * ∏P(xi|yk)
根据公式 P(yk|x) =P(yk) * ∏P(xi|yk) ，就可以做分类问题了。

拉普拉斯平滑

引入这个概率的意义，公式 P(yk|x) =P(yk) * ∏P(xi|yk)，是一个多项乘法公式，其中有一项数值为 0，则整个公式就为 0，显然不合理，避免每一项为零的做法就是，在分子、分母上各加一个数值。

P(y) = (|Dy| + 1) / (|D| + N)
参数说明：|Dy|表示分类 y 的样本数，|D|样本总数。
P(xi|Dy) = (|Dy,xi| + 1) / (|Dy| + Ni)
参数说明：|Dy,xi|表示分类 y 属性 i 的样本数，|Dy|表示分类 y 的样本数，Ni 表示 i 属性的可能的取值数。

文本分类

手动实现邮件分类

首先要对所有的已标记的邮件进行分词，整理得到每封邮件分词向量和全分词向量

根据邮件向量可以得到每个词在正常邮件中出现的概率（∏P(wi|Normal)）及垃圾邮件中出现的概率（∏P(wi|Spam)）

垃圾邮件的概率：P(spam)
正常邮件的概率：P(normal)
邮件是垃圾邮件的概率：
P(Spam|mail) = P(Spam) * ∏P(wi|Spam)
邮件是正常邮件的概率：
P(Normal|mail) = P(Normal) * ∏P(wi|Normal)

最后比较 P(Spam|mail) 与 P(Normal|mail) 的大小就可以了。

使用 sklearn 实现文本分类

# sklearn 实现文本分类
import os
import random 
from numpy import *
from numpy.ma import arange
from sklearn.pipeline import Pipeline
# TfidfVectorizer 文本特征提取（根据词出现的频率及在语句中的重要性）
# HashingVectorizer 文本的特征哈希
# CountVectorizer 将文本转换为每个词出现的个数的向量
 
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import BernoulliNB
from sklearn.naive_bayes import MultinomialNB
import matplotlib.pyplot as plt
 
# 获取样本集
def get_dataset():
    data = []
    for root, dirs, files in os.walk(r'./mix20_rand700_tokens_cleaned/tokens/neg'):
        for file in files:
            realpath = os.path.join(root, file)
            with open(realpath, errors='ignore') as f:
                data.append((f.read(), 'bad'))
    for root, dirs, files in os.walk(r'./mix20_rand700_tokens_cleaned/tokens/pos'):
        for file in files:
            realpath = os.path.join(root, file)
            with open(realpath, errors='ignore') as f:
                data.append((f.read(), 'good'))
    random.shuffle(data)
    return data
    
# 处理训练集与测试集
 
def train_and_test_data(data_):
    # 训练集和测试集的比例为 7:3
    filesize = int(0.7 * len(data_))
    # 训练集
    train_data_ = [each[0] for each in data_[:filesize]]
    train_target_ = [each[1] for each in data_[:filesize]]
    # 测试集
    test_data_ = [each[0] for each in data_[filesize:]]
    test_target_ = [each[1] for each in data_[filesize:]]
    return train_data_, train_target_, test_data_, test_target_
    
"""
多项式模型：
在多项式模型中， 设某文档 d=(t1,t2,…,tk)，tk 是该文档中出现过的单词，允许重复，则
先验概率 P(c)= 类 c 下单词总数 / 整个训练样本的单词总数
类条件概率 P(tk|c)=(类 c 下单词 tk 在各个文档中出现过的次数之和 +1)/(类 c 下单词总数 +|V|)
V 是训练样本的单词表（即抽取单词，单词出现多次，只算一个），|V|则表示训练样本包含多少种单词。 
P(tk|c) 可以看作是单词 tk 在证明 d 属于类 c 上提供了多大的证据，而 P(c) 则可以认为是类别 c 在整体上占多大比例 (有多大可能性)。
"""
def mnb(train_da, train_tar, test_da, test_tar):
    nbc = Pipeline([
        ('vect', TfidfVectorizer()),
        ('clf', MultinomialNB(alpha=1.0)),
    ])
    nbc.fit(train_da, train_tar)  # 训练我们的多项式模型贝叶斯分类器
    predict = nbc.predict(test_da)  # 在测试集上预测结果
    count = 0  # 统计预测正确的结果个数
    for left, right in zip(predict, test_tar):
        if left == right:
            count += 1
    # print(" 多项式模型：", count / len(test_target))
    return count / len(test_tar)
 
"""
伯努利模型：
P(c)= 类 c 下文件总数 / 整个训练样本的文件总数
P(tk|c)=(类 c 下包含单词 tk 的文件数 +1)/(类 c 下单词总数 +2)
"""
def bnb(train_da, train_tar, test_da, test_tar):
    nbc_1 = Pipeline([
        ('vect', TfidfVectorizer()),
        ('clf', BernoulliNB(alpha=1.0)),
    ])
    nbc_1.fit(train_da, train_tar)  # 训练我们的多项式模型贝叶斯分类器
    predict = nbc_1.predict(test_da)  # 在测试集上预测结果
 
    count = 0  # 统计预测正确的结果个数
    for left, right in zip(predict, test_tar):
        if left == right:
            count += 1
    # print(" 伯努利模型：", count / len(test_target))
    return count / len(test_tar)
 
# 训练十次
x = arange(10)
y1 = []
y2 = []for i in x:
    print(i)
    data = get_dataset()
    train_data, train_target, test_data, test_target = train_and_test_data(data)
    y1.append(mnb(train_data, train_target, test_data, test_target))
    y2.append(bnb(train_data, train_target, test_data, test_target))
 
print(x)
print(y1)
print(y2)
 
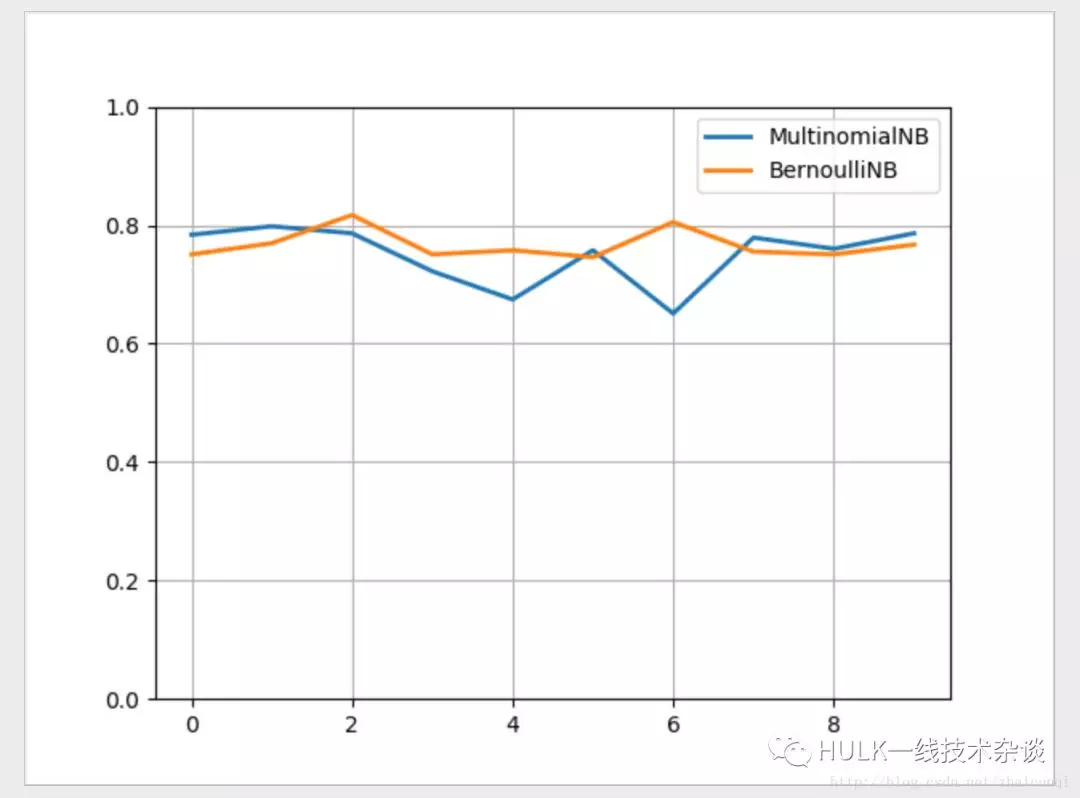
plt.plot(x, y1, lw='2', label='MultinomialNB')
plt.plot(x, y2, lw='2', label='BernoulliNB')
plt.legend(loc="upper right")
plt.ylim(0, 1)
plt.grid(True)
plt.show()

sklearn 结果对比

总结

Scikit learn 也简称 sklearn, 是机器学习领域当中最知名的 python 模块之一。Sklearn 把所有机器学习的模式整合统一起来了，学会了一个模式就可以通吃其他不同类型的学习模式。

本文转载自公众号 360 云计算（ID：hulktalk）。

原文链接：

https://mp.weixin.qq.com/s/maY1fp341KpJ3mMF1vefJQ