线性模型是机器学习中最基本的模型,既可以用来做回归任务,也可以用来做分类任务。这篇文章我们主要介绍用来做回归任务的线性回归。
线性模型主要有三个优点:
(1)形式简单,易于建模;
(2)作为机器学习最基础的模型,许多功能强大的非线性模型都是在线性模型的基础上加入层级结构或高维映射演进而来;
(3)具有良好的模型可解释性,权重 w 直观体现了各特征属性在预测中的重要性。
线性回归,顾名思义,就是通过学习得到一个特征的线性组合模型来预测连续值。
按特征(属性)数目,线性回归可以分为一元线性回归和多元线性回归:
一元线性回归模型 :
a 和 b 学得之后,模型就确定了,这里,自变量只有一个,所以该模型是平面上的一条直线。
多元线性回归模型 :
用向量形式改写为
w 是各自变量(特征属性)的权重,wi 绝对值越大,表明特征 xi 对于预测值影响越大,该模型自变量有多个,所以在空间上是一个平面。
学习策略及模型评估 :
如何求解自变量的权重 w 和 b 呢?通常采用极小化模型预测输出和真实值之间的距离,在回归任务中,采用基于均方误差最小化的“最小二乘法”来求解 w 和 b。
线性模型的评估主要使用均方误差、均方根误差、R-Square(被模型解释的信息比例)
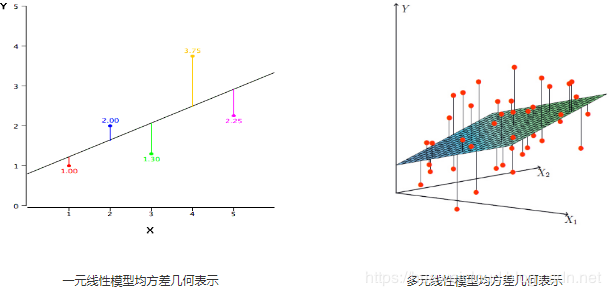
均方误差的几何意义:试图找到一条直线或一个平面,使得所有样本到直线上的欧式距离之和最小。如下图所示,分别表示一元线性模型和多元线性模型的均方差几何表示。
RMSE = M S E ( θ ^ ) = E ( ( θ ^ − θ ) 2 )
SSres 为拟合数据和原始数据的误差平方和,SStot 为原始数据和均值之差的平方和
多项式回归模型 :
现实问题中,直线或者平面并不能很好地拟合大部分数据,说明特征属性和预测值之间并没有很强的线性关系,我们需要采用多项式回归模型进行曲线或超平面拟合,这是一种特殊的线性模型,模型中自变量的指数大于 1,那就是多项式回归模型,一元多项式模型公式如下:
线性回归实战练习:
下面通过一个小的实战来对线性回归有一个更深入的理解,实战中上面提到的知识都会用到。我采用 sklearn 中自带的数据集 boston,该数据集包含对波士顿房价影响的多个特征属性值及对应的房价值,可以用来做回归任务的训练。
先看下数据的基本情况和有哪些特性:一共有 506 条数据,13 个特征属性
boston_data = datasets.load_boston()print (boston_data['data'].shape,"\n", boston_data['DESCR'])------------------------------------------------------------(506, 13) Boston House Prices dataset - CRIM per capita crime rate by town - ZN proportion of residential land zoned for lots over 25,000 sq.ft. - INDUS proportion of non-retail business acres per town - CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) - NOX nitric oxides concentration (parts per 10 million) - RM average number of rooms per dwelling - AGE proportion of owner-occupied units built prior to 1940 - DIS weighted distances to five Boston employment centres - RAD index of accessibility to radial highways - TAX full-value property-tax rate per $10,000
复制代码
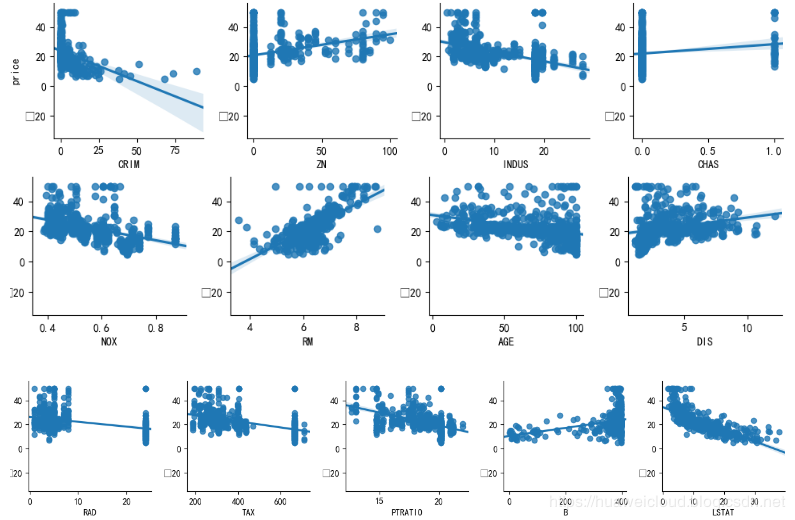
通过变量关系图看下各特征与预测值(房价)的相关性如何:
# 通过双变量关系图查看变量与预测值相关性data = pd.DataFrame(datasets.load_boston().data)data.columns = boston_data['feature_names']data['price'] = boston_data['target']sns.pairplot(data, x_vars=data.columns, y_vars='price', kind='reg')plt.show()
复制代码
从双变量关系图中可以看出,RM、LSTAT 这两个特征和房价的线性关系比较明显,其他特征的线性关系较弱。
先采用最简单的线性模型对数据进行预测,看效果怎么样。
def Evaluate_model(true_data_X, true_data_y, pred_data, model): # 计算MSE(均方差) print ("MSE:",metrics.mean_squared_error(true_data_y, pred_data)) # 计算RMSE(均方根差) print ("RMSE:",np.sqrt(metrics.mean_squared_error(true_data_y, pred_data))) # 模型R方 print ("R^2:", model.score(true_data_X, test_y)) data_np = boston_data['data']target_np = boston_data['target'] # 划分训练集和测试集train_X,test_X, train_y, test_y = train_test_split(data_np,target_np,test_size = 0.4,random_state = 0)model_linear = LinearRegression()model_linear.fit(train_X, train_y)# 预测y_pred_linear = model_linear.predict(test_X)# 模型评估Evaluate_model(test_X, test_y, y_pred_linear, model_linear)--------------------------------------------------------------MSE: 25.7971648592073RMSE: 5.079090948113382R^2: 0.6881784869675758
复制代码
从 baseline 模型的预测结果来看,效果并不是特别好,R-Squared 只有 0.68,对测试数据的拟合一般,从前面数据分析的变量关系图也可以看出,大部分特征和预测值之间并不是明显的线性关系,我们可以提高自变量的维度,也就是提高 x 的阶数,将模型变换为多项式回归模型。
# 多项式回归,最高阶设为2,阶数太高容易导致过拟合poly = PolynomialFeatures(degree=2, interaction_only=True,include_bias=True)train_X_poly = poly.fit_transform(train_X)test_X_poly = poly.transform(test_X)model_Polynomial = LinearRegression()model_Polynomial.fit(train_X_poly, train_y)y_pred_Polynomial = model_Polynomial.predict(test_X_poly) # 模型评估Evaluate_model(test_X_poly, test_y, y_pred_Polynomial, model_Polynomial)---------------------------------------------------------------------MSE: 17.989393685174065RMSE: 4.241390536743117R^2: 0.782554401304885
复制代码
看来预测房价,多项式回归模型比单纯的线性回归模型更适合,MSE 和 RMSE 都减少,并且 R-Squared 提升到 0.78,模型性能有较大程度的提升。
选定多项式回归模型后,还有没有方法继续优化提升模型性能呢?答案是正则化,正则化在数学推导上比较复杂,我们可以把它简单理解为一种特征选择方法,在模型中添加“惩罚系数”使得一些不那么重要的特征降低在模型中的影响度,常用的正则化方法有 Lasso 和 Ridge。
Lasso 方法倾向于压缩一部分特征的相关系数为 0,保留一小部分特征,通俗的理解就是如果两个特征变量如果强相关的话,Lasso 方法会将其中一个不那么重要特征的相关系数变为 0。而 Ridge 方法的做法则是尽量保留特征信息,只是把相关变量的系数同时缩小。
我尝试把两种正则化方法应用到模型中,看看效果如何
# 引入Lasso正则化model_lasso = LassoLarsCV()model_lasso.fit(train_X_poly, train_y)y_pred_lasso = model_lasso.predict(test_X_poly)# 模型评估Evaluate_model(test_X_poly, test_y, y_pred_lasso, model_lasso)----------------------------------------------------------MSE: 14.18038792061974RMSE: 3.765685584408202R^2: 0.8285955049352569---------------------------------------------------------# 引入Ridge正则化model_ridge = RidgeCV(alphas=[0.1, 1.0, 10.0])model_ridge.fit(train_X_poly, train_y)y_pred_ridge = model_ridge.predict(test_X_poly)# 模型评估Evaluate_model(test_X_poly, test_y, y_pred_ridge, model_ridge)-------------------------------------------------------------MSE: 15.737364846211017RMSE: 3.967034767456799R^2: 0.8097756499882447
复制代码
从预测的结果来看,正则化对模型预测率有一定帮助,如果特征属性非常多,而训练样本又比较少的情况下,正则化对应模型性能提升会有比较好的效果,最后,通过图形比较看看 baseline 模型和优化后引入 Lasso 正则化的模型,图中表示的是预测值 y 和真实值 x 的变化关系,离直线 y=x 越近的点表示预测准确度越高。从图上可以发现,引入 Lasso 方法的图形中,点明显更靠近直线,说明预测偏差更小,MSE、RMSE 和 R^Squared 等模型评估参数也说明了这一点。
作者简介 :
华为云专家周捷












评论