深度学习的数学（二）：神经元工作的数学表示

编者按：本文节选自图灵程序设计丛书 《深度学习的数学》一书中的部分章节。

如前文所述，神经网络是以从神经元抽象出来的数学模型为出发点的。下面，我们将更详细地考察神经元的工作，并将其在数学上抽象化。

整理神经元的工作

人的大脑是由多个神经元互相连接形成网络而构成的。也就是说，一个神经元从其他神经元接收信号，也向其他神经元发出信号。大脑就是根据这个网络上的信号的流动来处理各种各样的信息的。

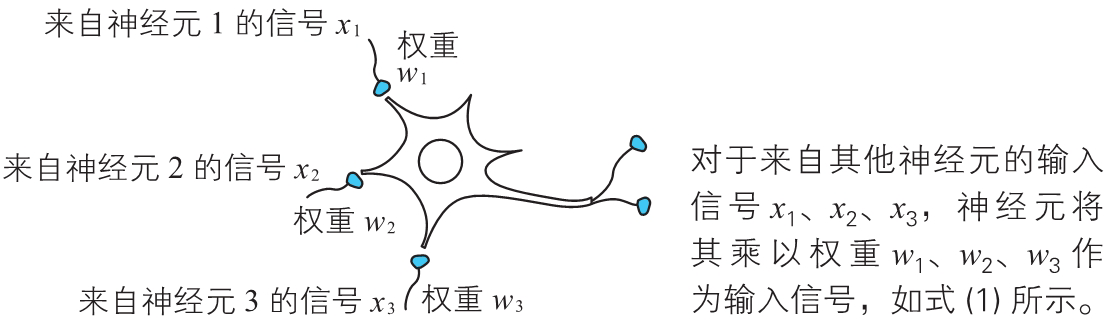
让我们来更详细地看一下神经元传递信息的结构。如上图所示，神经元是由细胞体、树突、轴突三个主要部分构成的。其他神经元的信号（输入信号）通过树突传递到细胞体（也就是神经元本体）中，细胞体把从其他多个神经元传递进来的输入信号进行合并加工，然后再通过轴突前端的突触传递给别的神经元。

那么，神经元究竟是怎样对输入信号进行合并加工的呢？让我们来看看它的构造。

假设一个神经元从其他多个神经元接收了输入信号，这时如果所接收的信号之和比较小，没有超过这个神经元固有的边界值（称为 阈值），这个神经元的细胞体就会忽略接收到的信号，不做任何反应。

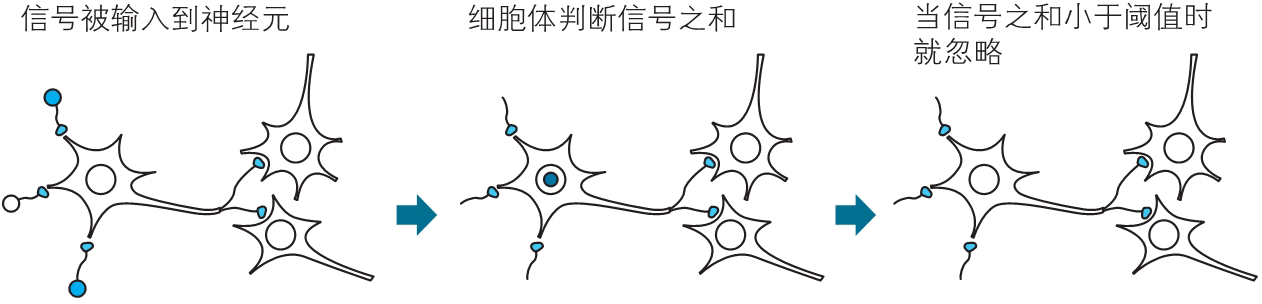
^{注：对于生命来说，神经元忽略微小的输入信号，这是十分重要的。反之，如果神经元对于任何微小的信号都变得兴奋，神经系统就将“情绪不稳定”。}

不过，如果输入信号之和超过神经元固有的边界值（也就是阈值），细胞体就会做出反应，向与轴突连接的其他神经元传递信号，这称为点火。

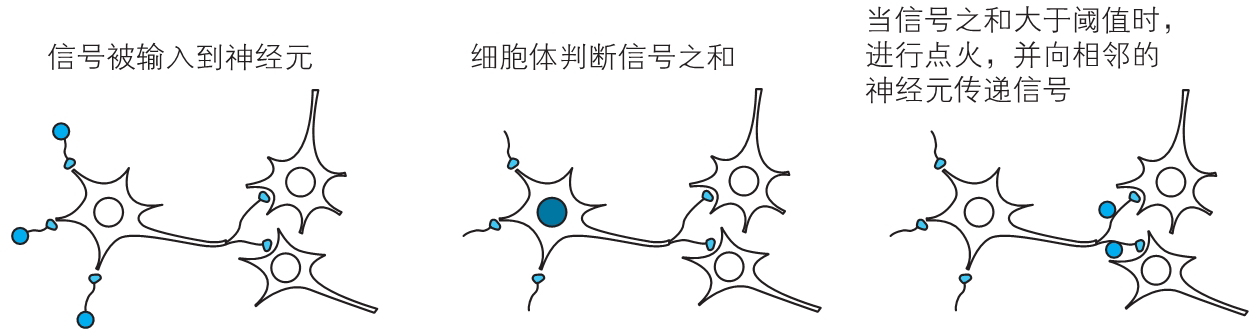
那么，点火时神经元的输出信号是什么样的呢？有趣的是，信号的大小是固定的。即便从邻近的神经元接收到很大的刺激，或者轴突连接着其他多个神经元，这个神经元也只输出固定大小的信号。点火的输出信号是由 0 或 1 表示的数字信息。

神经元工作的数学表示

让我们整理一下已经考察过的神经元点火的结构。

(i)　来自其他多个神经元的信号之和成为神经元的输入。

(ii)　如果这个信号之和超过神经元固有的阈值，则点火。

(iii)　神经元的输出信号可以用数字信号 0 和 1 来表示。即使有多个输出端，其值也是同一个。

下面让我们用数学方式表示神经元点火的结构。

首先，我们用数学式表示输入信号。由于输入信号是来自相邻神经元的输出信号，所以根据 (iii)，输入信号也可以用“有”“无”两种信息表示。因此，用变量 $x$ 表示输入信号时，如下所示。

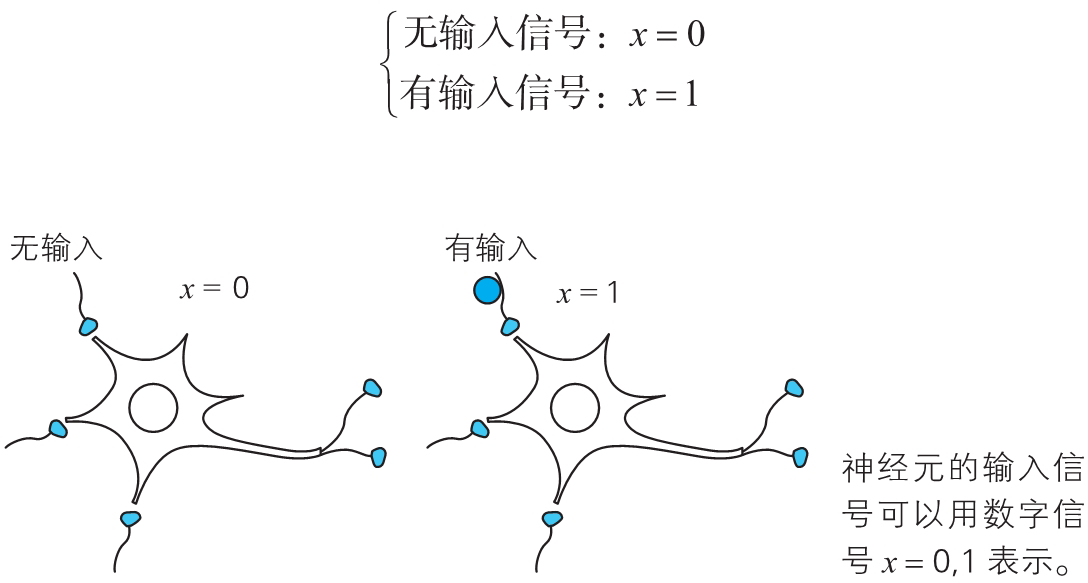
^{注：与视细胞直接连接的神经元等个别神经元并不一定如此，因为视细胞的输入是模拟信号。}

接下来，我们用数学式表示输出信号。根据 (iii)，输出信号可以用表示点火与否的“有”“无”两种信息来表示。因此，用变量 $y$ 表示输出信号时，如下所示。

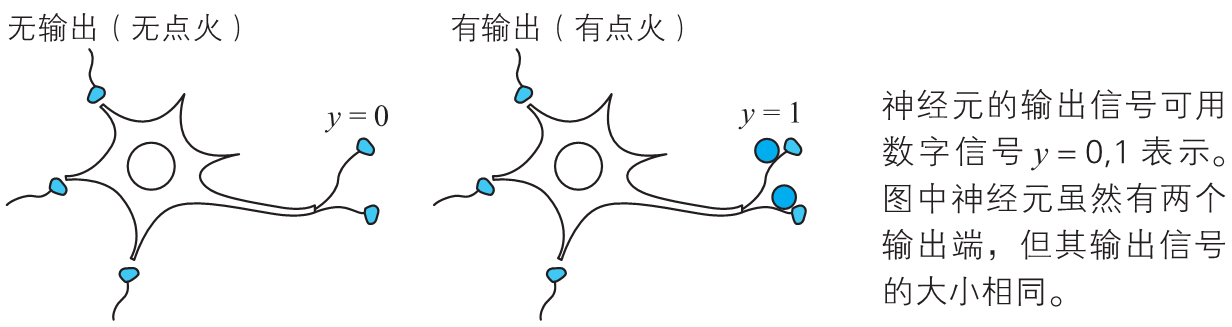
最后，我们用数学方式来表示点火的判定条件。

从 (i) 和 (ii) 可知，神经元点火与否是根据来自其他神经元的输入信号的和来判定的，但这个求和的方式应该不是简单的求和。例如在网球比赛中，对于来自视觉神经的信号和来自听觉神经的信号，大脑是通过改变权重来处理的。因此，神经元的输入信号应该是考虑了权重的信号之和。用数学语言来表示的话，例如，来自相邻神经元 1、2、3 的输入信号分别为 $x_1$、$x_2$、$x_3$，则神经元的输入信号之和可以如下表示。

式中的 $w_1$、$w_2$、$w_3$ 是输入信号 $x_1$、$x_2$、$x_3$ 对应的 权重（weight）。

根据 (ii)，神经元在信号之和超过阈值时点火，不超过阈值时不点火。于是，利用式 (1)，点火条件可以如下表示。

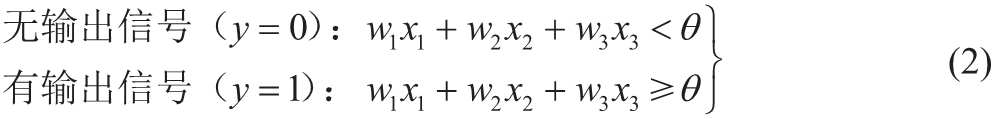
这里，$\theta$ 是该神经元固有的阈值。

例 1 来自两个神经元 1、2 的输入信号分别为变量 $x_1$、$x_2$，权重为 $w_1$、$w_2$，神经元的阈值为 $\theta$。当 $w_1=5$，$w_2=3$，$\theta =4$ 时，考察信号之和 $w_1{x}_1+w_2{x}_2$ 的值与表示点火与否的输出信号 $y$ 的值。

点火条件的图形表示

下面我们将表示点火条件的式 (2) 图形化。以神经元的输入信号之和为横轴，神经元的输出信号 $y$ 为纵轴，将式 (2) 用图形表示出来。如下图所示，当信号之和小于 $\theta$ 时，$y$ 取值 0，反之 $y$ 取值 1。

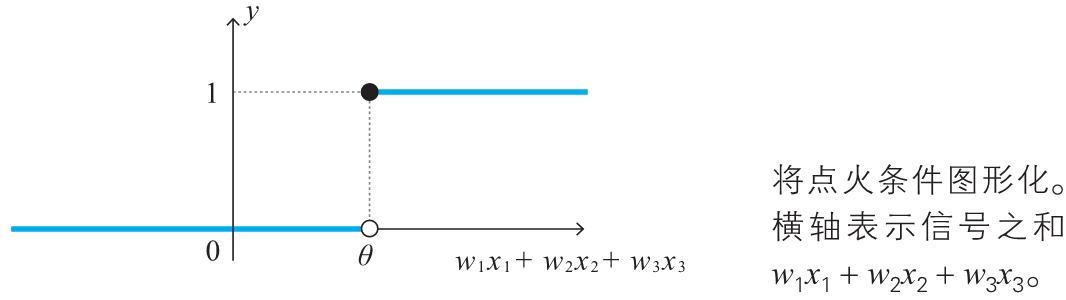
如果用函数式来表示这个图形，就需要用到下面的 单位阶跃函数。

单位阶跃函数的图形如下所示。

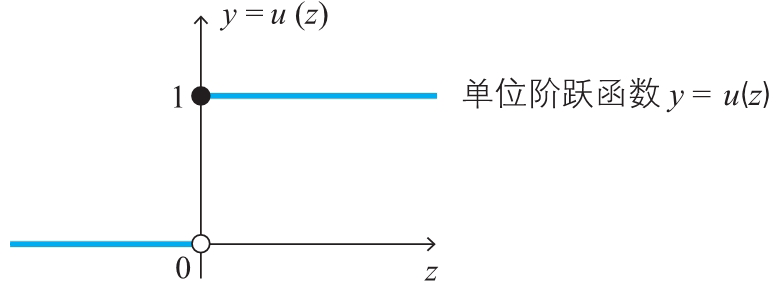
利用单位阶跃函数 $u(z)$，式 (2) 可以用一个式子表示如下。

点火的式子：$y=u(w_1{x}_1+w_2{x}_2+w_3{x}_3-\theta )(3)$

通过下表可以确认式 (3) 和式 (2) 是一样的。

|$\mathbf{y}$|${\mathbf{w}}_1{\mathbf{x}}_1+{\mathbf{w}}_2{\mathbf{x}}_2+{\mathbf{w}}_3{\mathbf{x}}_3$|$\mathbf{z}={\mathbf{w}}_1{\mathbf{x}}_1+{\mathbf{w}}_2{\mathbf{x}}_2+{\mathbf{w}}_3{\mathbf{x}}_3-\theta$|$\mathbf{u}(\mathbf{z})$|

|-|-|

|0（无点火）|小于 $\theta$|$z<0$|0|

|1（点火）|大于等于 $\theta$|$z⩾0$|1|

此外，该表中的 $z$（式　(3) 的阶跃函数的参数）的表达式

称为该神经元的 加权输入。

备注 ${\mathbf{w}}_1{\mathbf{x}}_1+{\mathbf{w}}_2{\mathbf{x}}_2+{\mathbf{w}}_3{\mathbf{x}}_3=\theta$ 的处理

有的文献会像下面这样处理式 (2) 的不等号。

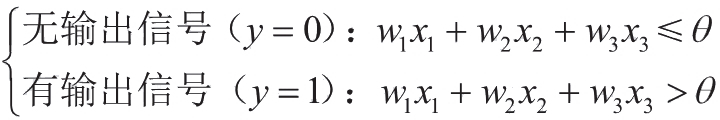
在生物上这也许是很大的差异，不过对于接下来的讨论而言是没有问题的。因为我们的主角是 Sigmoid 函数，所以不会发生这样的问题。

图书简介：http://www.ituring.com.cn/book/2593

相关阅读

深度学习的数学（一）：神经网络和深度学习