引言
早在 1990 年,Leslie Lamport(即 LaTeX 中的"La",微软研究院科学家,获得 2013 年图灵奖)向 ACM Transactions on Computer Systems (TOCS) 提交了关于 Paxos 算法的论文 _The Part-Time Parliament_。几位审阅人表示,虽然论文没什么特别的用处,但还是有点意思,只是要把 Paxos 相关的故事背景全部删掉。Leslie Lamport 心高气傲,觉得审阅人没有丝毫的幽默感,于是撤回文章不再发表。直到 1998 年,用户开始支持 Paxos,Leslie Lamport 重新发表文章,但相比 1990 年的版本,文章没有太大的修改,所以还是不好理解。于是在 2001 年,为了通俗性,Leslie Lamport 简化文章发表了 _Paxos Made Simple_,这次文中没有一个公式。
但事实如何?大家不妨读一读 _Paxos Made Simple_。Leslie Lamport 在文中渐进式地、从零开始推导出了 Paxos 协议,中间用数学归纳法进行了证明。可能是因为表述顺序的问题,导致这篇文章似乎还是不好理解。
于是,基于此背景,本文根据 _Paxos Made Simple_,重新描述 Paxos 协议,提供两种证明方法,给出常见的理解误区。期望读者通过阅读本文,再结合 _Paxos Made Simple_,就可以深入理解基本的 Paxos 协议理论。
基本概念
- Proposal Value:提议的值;
- Proposal Number:提议编号,要求提议编号不能冲突;
- Proposal:提议 = 提议的值 + 提议编号;
- Proposer:提议发起者;
- Acceptor:提议接受者;
- Learner:提议学习者。
注意,提议跟提议的值是有区别的,后面会具体说明。协议中 Proposer 有两个行为,一个是向 Acceptor 发 Prepare 请求,另一个是向 Acceptor 发 Accept 请求;Acceptor 则根据协议规则,对 Proposer 的请求作出应答;最后 Learner 可以根据 Acceptor 的状态,学习最终被确定的值。
方便讨论,在本文中,记{n,v}为提议编号为 n,提议的值为 v 的提议,记 (m,{n,v}) 为承诺了 Prepare(m)请求,并接受了提议{n,v}。
协议过程
第一阶段 A
Proposer 选择一个提议编号 n,向所有的 Acceptor 广播 Prepare(n)请求。
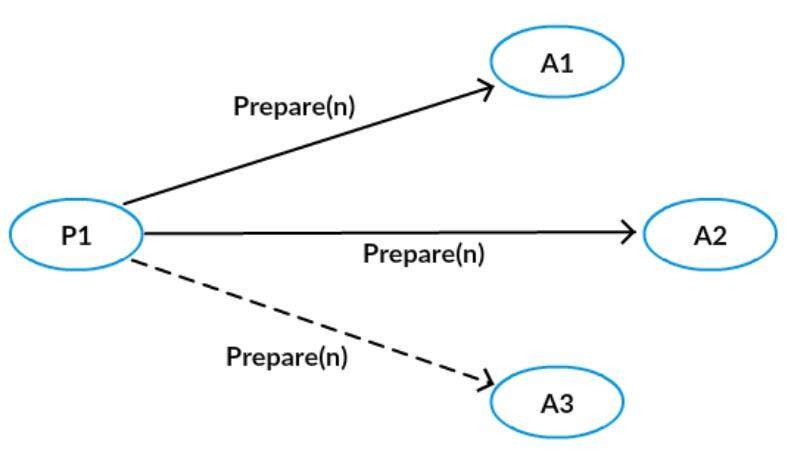
第一阶段 B
Acceptor 接收到 Prepare(n)请求,若提议编号 n 比之前接收的 Prepare 请求都要大,则承诺将不会接收提议编号比 n 小的提议,并且带上之前 Accept 的提议中编号小于 n 的最大的提议,否则不予理会。
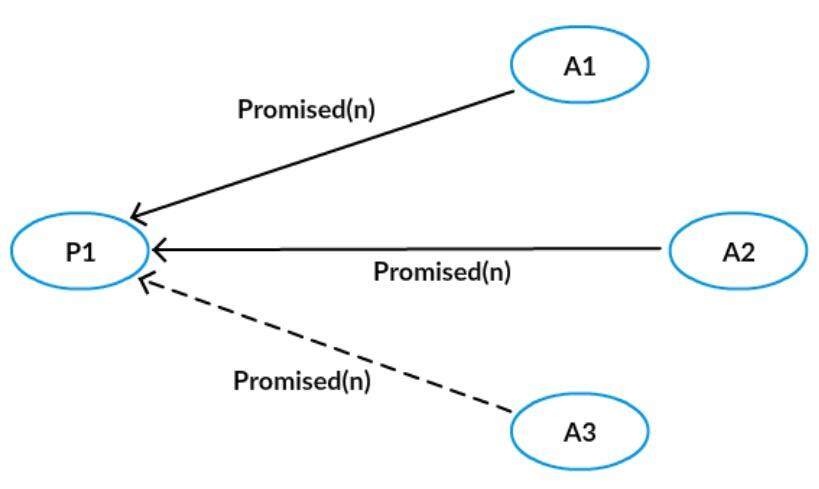
第二阶段 A
Proposer 得到了多数 Acceptor 的承诺后,如果没有发现有一个 Acceptor 接受过一个值,那么向所有的 Acceptor 发起自己的值和提议编号 n,否则,从所有接受过的值中选择对应的提议编号最大的,作为提议的值,提议编号仍然为 n。
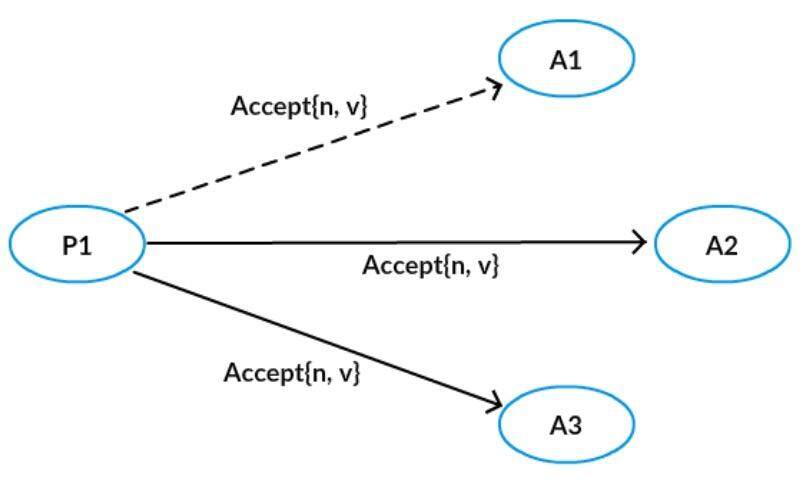
第二阶段 B
Acceptor 接收到提议后,如果该提议编号不违反自己做过的承诺,则接受该提议。
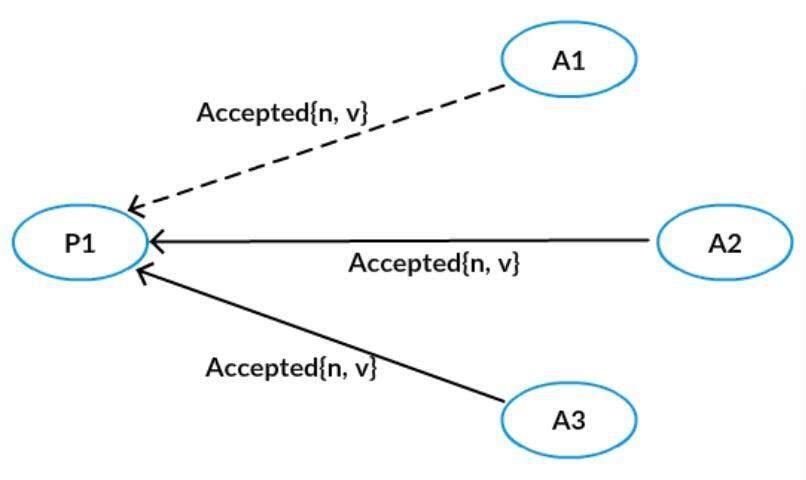
需要注意的是,Proposer 发出 Prepare(n)请求后,得到多数派的应答,然后可以随便再选择一个多数派广播 Accept 请求,而不一定要将 Accept 请求发给有应答的 Acceptor,这是常见的 Paxos 理解误区。
小结
上面的图例中,P1 广播了 Prepare 请求,但是给 A3 的丢失,不过 A1、A2 成功返回了,即该 Prepare 请求得到多数派的应答,然后它可以广播 Accept 请求,但是给 A1 的丢了,不过 A2,A3 成功接受了这个提议。因为这个提议被多数派(A2,A3 形成多数派)接受,我们称被多数派接受的提议对应的值被 Chosen。
三个 Acceptor 之前都没有接受过 Accept 请求,所以不用返回接受过的提议,但是如果接受过提议,则根据第一阶段 B,要带上之前 Accept 的提议中编号小于 n 的最大的提议。
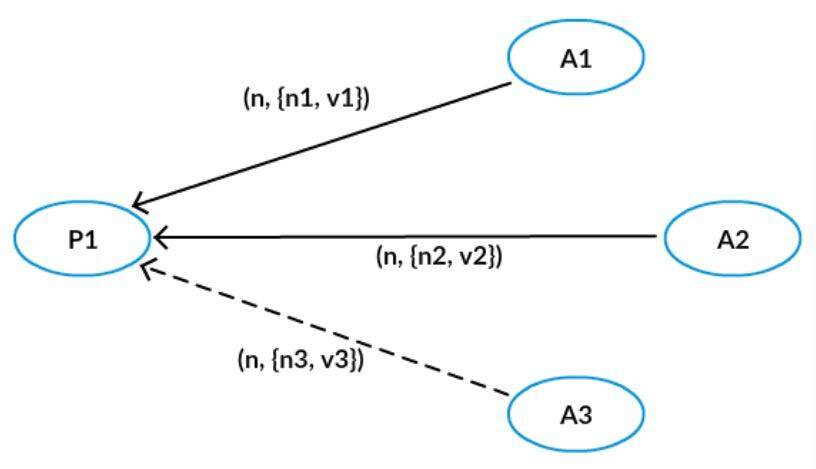
Proposer 广播 Prepare 请求之后,收到了 A1 和 A2 的应答,应答中携带了它们之前接受过的{n1, v1}和{n2, v2},Proposer 则根据 n1,n2 的大小关系,选择较大的那个提议对应的值,比如 n1 > n2,那么就选择 v1 作为提议的值,最后它向 Acceptor 广播提议{n, v1}。
Paxos 协议最终解决什么问题
当一个提议被多数派接受后,这个提议对应的值被 Chosen(选定),一旦有一个值被 Chosen,那么只要按照协议的规则继续交互,后续被 Chosen 的值都是同一个值,也就是这个 Chosen 值的一致性问题。
协议证明
上文就是基本 Paxos 协议的全部内容,其实是一个非常确定的数学问题。下面用数学语言表达,进而用严谨的数学语言加以证明。
Paxos 原命题
如果一个提议{n0,v0}被大多数 Acceptor 接受,那么不存在提议{n1,v1}被大多数 Acceptor 接受,其中 n0 < n1,v0 != v1。
Paxos 原命题加强
如果一个提议{n0,v0}被大多数 Acceptor 接受,那么不存在 Acceptor 接受提议{n1,v1},其中 n0 < n1,v0 != v1。
Paxos 原命题进一步加强
如果一个提议{n0,v0}被大多数 Acceptor 接受,那么不存在 Proposer 发出提议{n1,v1},其中 n0 < n1,v0 != v1。
如果“Paxos 原命题进一步加强”成立,那么“Paxos 原命题”显然成立。下面我们通过证明“Paxos 原命题进一步加强”,从而证明“Paxos 原命题”。论文中是使用数学归纳法进行证明的,这里用比较紧凑的语言重新表述证明过程。
归纳法证明
假设,提议{m,v}(简称提议 m)被多数派接受,那么提议 m 到 n(如果存在)对应的值都为 v,其中 n 不小于 m。
这里对 n 进行归纳假设,当 n = m 时,结论显然成立。
设 n = k 时结论成立,即如果提议{m,v}被多数派接受,
那么提议 m 到 k 对应的值都为 v,其中 k 不小于 m。
当 n = k+1 时,若提议 k+1 不存在,那么结论成立。
若提议 k+1 存在,对应的值为 v1,
因为提议 m 已经被多数派接受,又 k+1 的 Prepare 被多数派承诺并返回结果。
基于两个多数派必有交集,易知提议 k+1 的第一阶段 B 有带提议回来。
那么 v1 是从返回的提议中选出来的,不妨设这个值是选自提议{t,v1}。
根据第二阶段 B,因为 t 是返回的提议中编号最大,所以 t >= m。
又由第一阶段 A,知道 t < n。所以根据假设 t 对应的值为 v。
即有 v1 = v。所以由 n = k 结论成立,可以推出 n = k+1 成立。
于是对于任意的提议编号不小于 m 的提议 n,对应的值都为 v。
所以命题成立。
反证法证明
假设存在,不妨设 n1 是满足条件的最小提议编号。
即存在提议{n1,v1},其中 n0 < n1,v0 != v1。-------------(A)
那么提议 n0,n0+1,n0+2,…,n1-1 对应的值为 v0。-------------(B)
由于存在提议{n1,v1},则说明大多数 Acceptor 已经接收 n1 的 Prepare,并承诺将不会接受提议编号比 n1 小的提议。
又因为{n0,v0}被大多数 Acceptor 接受,
所以存在一个 Acceptor 既对 n1 的 Prepare 进行了承诺,又接受了提议 n0。
由协议的第二阶段 B 知,这个 Acceptor 先接受了{n0,v0}。
所以发出{n1,v1}提议的 Proposer 会从大多数的 Acceptor 返回中得知,
至少某个编号不小于 n0 而且值为 v0 的提议已经被接受。-------------(C)
由协议的第二阶段 A 知,
该 Proposer 会从已经被接受的值中选择一个提议编号最大的,作为提议的值。
由(C)知该提议编号不小于 n0,由协议第二阶段 B 知,该提议编号小于 n1,
于是由(B)知 v1 == v0,与(A)矛盾。
所以命题成立。
通过上面的证明过程,我们反过来回味一下协议中的细节。
- 为什么要被多数派接受?因为两个多数派之间必有交集,所以 Paxos 协议一般是 2F+1 个 Acceptor,然后允许最多 F 个 Acceptor 停机,而保证协议依然能够正常进行,最终得到一个确定的值。
- 为什么需要做一个承诺?可以保证第二阶段 A 中 Proposer 的选择不会受到未来变化的干扰。另外,对于一个 Acceptor 而言,这个承诺决定了它回应提议编号较大的 Prepare 请求,和接受提议编号较小的 Accept 请求的先后顺序。
- 为什么第二阶段 A 要从返回的协议中选择一个编号最大的?这样选出来的提议编号一定不小于已经被多数派接受的提议编号,进而可以根据假设得到该提议编号对应的值是 Chosen 的那个值。
原文的第一阶段 B
Acceptor 接收到 Prepare(n)请求,若提议编号 n 比之前接收的 Prepare 请求都要大,则承诺将不会接收提议编号比 n 小的提议,并且带上之前 Accept 的提议中编号最大的提议,否则不予理会。
相对上面的表达少了“比 n 小的”,通过邮件向 Leslie Lamport 请教了这个问题,他表示接受一个提议,包含回应了一个 Prepare 请求。这个有点隐晦,但也完全合理,有了这个条件,上面的证明也就通顺了。就是说 Acceptor 接受过的提议的编号总是不大于承诺过的提议编号,于是可以将这个“比 n 小的”去掉,在实际工程实践中我们往往只保存接受过的提议中编号最大的,以及承诺过的 Prepare 请求编号最大的。
Leslie Lamport 也表示在去掉“比 n 小的”的情况下,就算接受一个提议不包含回应一个 Prepare 请求,最终结论也是对的,因为前者明显可以推导出后者,去掉反而把条件加强了。
假如返回的提议中有编号大于 n 的,比如{m,v},那么肯定存在多数派承诺拒绝小于 m 的 Accept 请求,所以提议{n,v}不可能被多数派接受。
学习过程
如果一个提议被多数 Acceptor 接受,则这个提议对应的值被选定。
一个简单直接的学习方法就是,获取所有 Acceptor 接受过的提议,然后看哪个提议被多数的 Acceptor 接受,那么该提议对应的值就是被选定的。
另外,也可以把 Learner 看作一个 Proposer,根据协议流程,发起一个正常的提议,然后看这个提议是否被多数 Acceptor 接受。
这里强调“一个提议被多数 Acceptor 接受”,而不是“一个值被多数 Acceptor”接受,如果是后者会有什么问题?
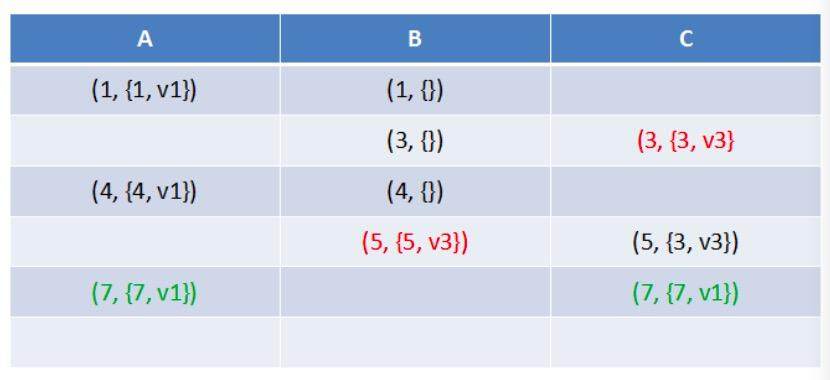
提议{3,v3},{5,v3}分别被 B、C 接受,即有 v3 被多数派接受,但不能说明 v3 被选定(Chosen),只有提议{7,v1}被多数派(A 和 C 组成)接受,我们才能说 v1 被选定,而这个选定的值随着协议继续进行不会改变。
总结
“与其预测未来,不如限制未来”,这应该是 Paxos 协议的核心思想。如果你在阅读 Paxos 的这篇论文时感到困惑,不妨找到“限制”的段落回味一番。Paxos 协议本身是比较简单的,如何将 Paxos 协议工程化,才是真正的难题。
目前在微信核心存储 PaxosStore 中,每分钟调用 Paxos 协议过程数十亿次量级,而《微信 PaxosStore 内存云揭秘:十亿 Paxos/ 分钟的挑战》一文, 则对内存云子系统做了展开。
后续我们将发表更多的实践方案,包括万亿级别的海量闪存存储,支持单表亿行的 NewSQL 解决方案,以及有别于业界的开源实现,PaxosStore 架构方案基于非租约的 Paxos 实现等内容。
作者介绍
郑建军,微信工程师,目前负责微信基础存储服务,致力于强一致、高可用的大规模分布式存储系统的设计与研发。
感谢陈兴璐对本文的审校。
给InfoQ 中文站投稿或者参与内容翻译工作,请邮件至 editors@cn.infoq.com 。也欢迎大家通过新浪微博( @InfoQ , @丁晓昀),微信(微信号: InfoQChina )关注我们。




