前言
回顾一下 通俗易懂的红黑树图解(上),上篇首先介绍了二叉树的定义以及二叉树的查找,然后介绍了红黑树的五点性质以及红黑树的变色、左旋以及右旋等操作,最后结合变色、左旋及右旋详细讲解了插入节点的五种场景。而本篇通俗易懂的红黑树图解(下)是在上篇的基础上讲解红黑树最后一种操作-删除节点,删除节点相对插入节点会复杂一点,但通过分类归纳出不同的场景,能更容易理解和记忆。
○ 红黑树删除
红黑树删除操作包括两部分,一是查找到删除节点,二是删除节点以及删除之后的自平衡。查找节点与二叉树的查找方式一样。而删除操作,当删除节点不存在时,结束本次删除操作;当删除节点存在时,删除节点,然后找到一个节点替换已删除的节点位置,重新连接上已删除节点的父节点与孩子节点。
如下图,删除节点 D ,需要找到一个节点可以替换到 D 节点位置,否则节点 P 和节点 L 及 R 之间的链接会断开,破坏了红黑树的性质,形成独立的树形结构。

关键字:查找节点 替换节点
○ 查找节点
查找删除节点与 二叉树查找节点 (https://juejin.im/post/5dff59cb6fb9a0163c53ce1d#heading-8) 逻辑相同,通过与当前节点值比较,返回当前节点或者继续从左子树或者右子树继续查找。
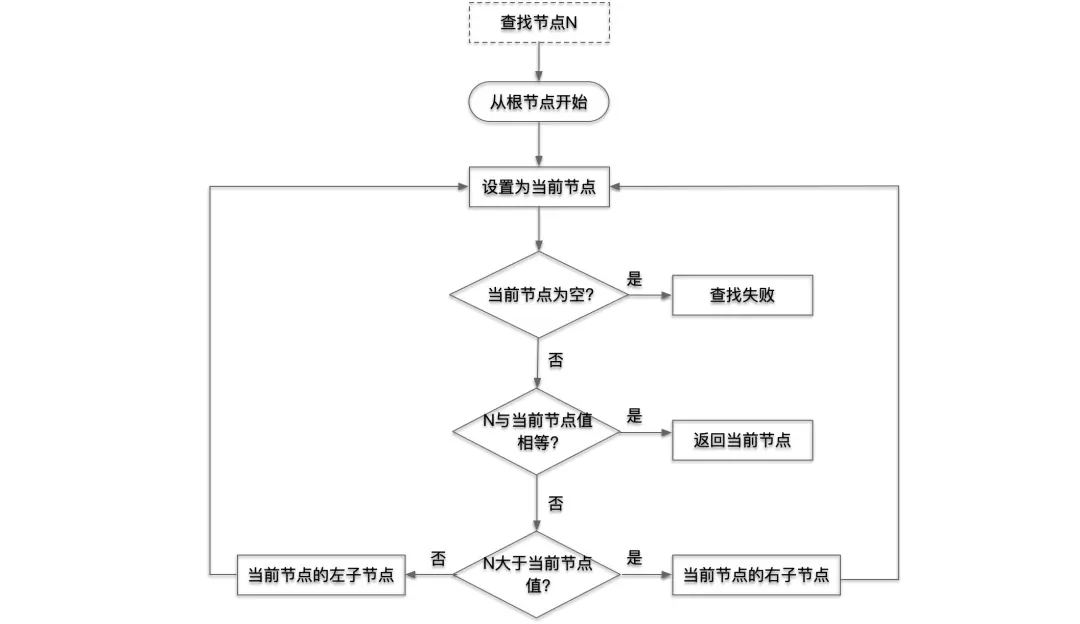
在二叉查找树中查找节点 N ,首先从根节点开始,将根节点设置为当前节点,若当前节点为空,则查找失败,若 N 与当前节点值相等,返回当前节点,若 N 大于当前节点值,则从当前节点的右子节点开始查找,否则从当前节点的左子节点开始查找,直到返回目标节点或者查找失败;
○ 替换节点
回顾一下二叉查找树的性质:
若任意节点左子树不为空,它的左子树上所有节点值均小于它的根节点的值
若任意节点的右子树不为空,它的右子树上所有节点的值均大于它的根节点的值
根据二叉查找树的性质,删除节点之后,可以找到两个替换节点,即可以用左子树中的最大值以及右子树中的最小值来替换删除节点。
删除节点找替换节点又分三种情景:
情景 1:删除节点无子节点,可以直接删除,无需替换
情景 2:删除节点只有一个子节点,用子节点替换删除节点
情景 3:删除节点有两个子节点,可以用后继节点或者前继节点替换删除节点。本文采用前者,即后继节点替换删除节点
后继节点:删除节点的右子树中的最小节点,即右子树中最左节点。
前继节点:删除节点的左子树中最大节点,即左子树中最右节点。
综上所述,寻找一个节点替换已删除节点位置,在不考虑节点值情况下,可等同于删除替换节点。
○ 节点删除
删除节点可等同于删除替换节点,所以节点删除就转换到了替换节点的各种场景。节点删除又分 9 种场景,在如下的描述场景中,场景 2 中的四种情况与场景 3 中的四种情况分别互为镜像,可参照对比着看。
删除场景 1:替换节点是红色节点
即替换的节点是红色节点,删除之后不影响红黑树的平衡,只需要把替换节点的颜色设成被删除节点的颜色即可重新平衡。
处理: 删除节点 D,查找到替换节点 R,R 设成 D 节点的颜色,再替换 D 节点位置。

删除场景 2:替换节点是黑色节点、且是其父节点的左子节点
替换节点是黑色节点时,删除之后破坏了红黑树的平衡,需要考虑自平衡处理。而此又细分为 4 种场景。
场景 2.1:替换节点的兄弟节点是红色。删除黑色节点,左子树中黑色节点数减少一个,可以通过一些操作,达到间接借用红色的兄弟节点来补充左子树中黑色节点数。
处理:替换节点的父节点 P 设置红色、兄弟节点 S 设置成黑色,再对节点 P 左旋操作,变成场景 2.4。

场景 2.2:替换节点的兄弟节点是黑色且兄弟节点的右子节点是红色、左子节点任意颜色。同样是间接借用兄弟节点的红色右子节点补充到左子树中,达到红黑树的平衡。
处理:替换节点的兄弟节点 S 设置成父节点 P 的颜色,兄弟节点的右子节点 SR 设置为黑色,父节点 P 设置为黑色,再对节点 P 左旋操作。此时节点 R 替换到删除节点位置之后,红黑树重新达到平衡状态。

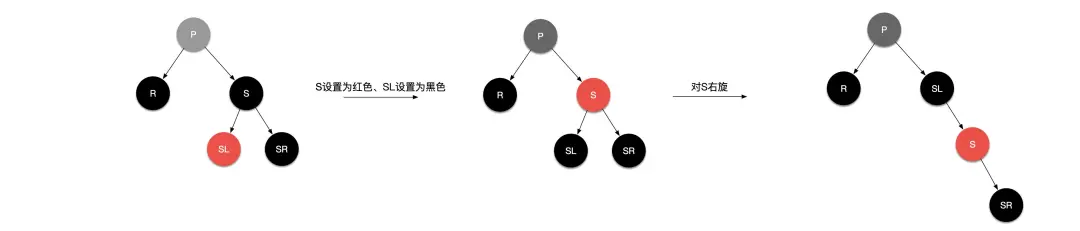
场景 2.3:替换节点的兄弟节点是黑色且兄弟节点的左子节点是红色,右子节点是黑色。
处理:替换节点的兄弟节点 S 设置成红色,兄弟节点的左子节点 SL 设置为黑色,再对节点 S 右旋操作,转换到了场景 2.2,再进行场景 2.2 的操作。
场景 2.4:替换节点的兄弟节点的左右子节点都是黑色。兄弟节点的子节点不能借用,就只能借用兄弟节点了。
处理:替换节点的兄弟节点 S 设置成红色,以父节点 P 当作替换节点,然后自底向上处理。

场景 3:替换节点是黑色节点、且是其父节点的右子节点。(与场景 2 镜像)
场景 3.1:替换节点的兄弟节点是红色。
处理:替换节点的父节点 P 设置红色、兄弟节点 S 设置成黑色,再对节点 P 右旋操作,变成场景 3.4。

场景 3.2:替换节点的兄弟节点是黑色且兄弟节点的左子节点是红色、右子节点任意颜色。
处理:替换节点的兄弟节点 S 设置成父节点 P 的颜色,兄弟节点的左子节点 SL 设置为黑色,父节点 P 设置为黑色,再对节点 P 右旋操作。此时节点 R 替换到删除节点位置之后,红黑树重新达到平衡状态。

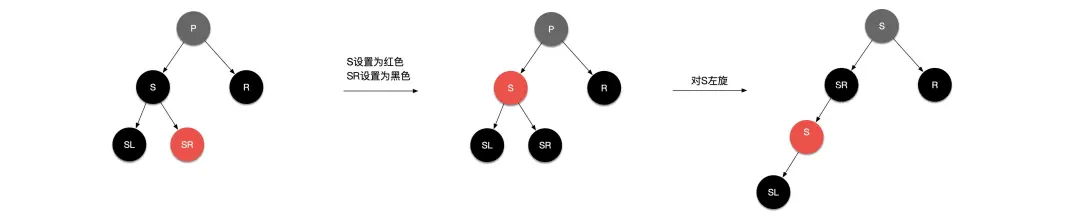
场景 3.3:替换节点的兄弟节点是黑色且兄弟节点的右子节点是红色、左子节点为黑色。
处理:替换节点的兄弟节点 S 设置成红色,兄弟节点的右子节点 SL 设置为黑色,再对节点 S 左旋操作,转换到了场景 3.2,再进行场景 3.2 的操作。
场景 3.4:替换节点的兄弟节点的左右子节点都是黑色。
处理:替换节点的兄弟节点 S 设置成红色,以父节点 P 当作替换节点,然后自底向上处理。

节点删除及平衡代码:
/** * 查找节点 * @param key 节点key值 */search(key) { let node = this.root while (node) { if (key < node.key) { node = node.left } else if (key > node.key) { node = node.right } else if (key === node.key) { break } } return node}/** * 替换u节点,重置v节点 * @param u 待删除节点 * @param v 子节点 */const replace = function(u, v) { if(!u.parent){ // u是根节点,设置v为根节点 this.root = v } else if(u === u.parent.left){ // 重置u的父节点的左节点 u.parent.left = v } else { // 重置u的父节点的右节点 u.parent.right = v } // 重置v的父节点 v.parent = u.parent} /** * 查找node节点的后继节点 */ findSuccessor(node) { while (node.left) { node = node.left; } return node; }/** * 删除节点 * @param key 删除节点key值 */delete(key) { const node = search(key) if(!node){ return } let fix let color = node.color if(!node.left){ //左节点为空值 fix = node.right this.replace(node, node.right) } else if(!node.right){ //右节点为空值 fix = node.left this.replace(node, node.left) } else { // 左右节点都不为空值 const successor = this.findSuccessor(node.right) //替换节点的颜色 color = successor.color //后继节点只存在右节点或者两个nil子节点情况 fix = successor.right //如果后继节点是父节点的非直接子节点 if(successor.parent !== node){ this.replace(successor, successor.right) successor.right = node.right successor.right.parent = successor } this.replace(node, successor) successor.color = node.color successor.left = node.left successor.left.parent = successor } if(color === Color.BLACK){ this.balanceDeletion(fix) }}/** * 删除节点平衡修正 * @param node 节点 */ balanceDeletion(node) { while (node !== this.root && node.color === Color.BLACK) { // 节点是父节点的左子节点 if (node === node.parent.left) { //兄弟节点 let sibling = node.parent.right; if (sibling.color === Color.RED) { // 场景2.1:兄弟节点是红色 // 兄弟节点设置为黑色 sibling.color = Color.BLACK; //替换节点的父节点设置为红色 node.parent.color = Color.RED; // 左旋 this.rotateLeft(node.parent); sibling = node.parent.right; } if (sibling.left.color === Color.BLACK && sibling.right.color === Color.BLACK) { // 场景2.4: 兄弟节点两个子节点都是黑色 sibling.color = Color.RED; //再次以父节点为新节点作自平衡处理。 node = node.parent; continue; } else if (sibling.left.color === Color.RED) { // 场景2.3: 兄弟节点的左子节点是黑色,转换到场景2.2. sibling.left.color = Color.BLACK; sibling.color = Color.RED; //对兄弟节点右旋 this.rotateRight(sibling) sibling = node.parent.right; } if (sibling.right.color === Color.RED) { //场景2.2:兄弟节点的右节点是红色 sibling.color = node.parent.color; node.parent.color = Color.BLACK; sibling.right.color = Color.BLACK; //对父节点左旋 this.rotateLeft(node.parent); // 左旋之后,红黑树重新平衡 node = this.root; } } else { //节点是父节点的左节点 let sibling = node.parent.left; if (sibling.color === Color.RED) { // 场景 3.1:替换节点的兄弟节点是红色 sibling.color = Color.BLACK; node.parent.color = Color.RED; this.rotateRight(node.parent); sibling = node.parent.left; } if (sibling.right.color === Color.BLACK && sibling.left.color === Color.BLACK) { //场景3.4:替换节点的两个子节点都是黑色 sibling.color = Color.RED; //再次以父节点为新节点作自平衡处理。 node = node.parent; continue } else if (sibling.right.color === Color.RED) { // 场景3.3:兄弟节点的右子节点是红色 sibling.right.color = Color.BLACK; sibling.color = Color.RED; this.rotateLeft(sibling); sibling = node.parent.left; } if (sibling.left.color === Color.RED) { // 场景3.2:兄弟节点的左子节点是红色 sibling.color = node.parent.color; node.parent.color = Color.BLACK; sibling.left.color = Color.BLACK; this.rotateRight(node.parent); node = this.root; } } } node.color = Color.BLACK; }}红黑树应用
红黑树广泛用在 Java 的集合框架 (HashMap、TreeMap、TreeSet)、Nginx 的 Timer 管理、Linux 虚拟内存管理以及 C++ 的 STL 等等场景。
在 Linux 内核中,每个用户进程都可以访问 4GB 的线性虚拟空间,虚拟空间往往需要多个虚拟内存区域描述,对这些内存区域,Linux 内核采用了链表以及红黑树形式组织。内存区域按地址排序,链接成一个链表以及一颗红黑树,寻找空闲区域时只需要遍历这个链表,在发生缺页中断时通过红黑树快速检索特定内存区域。
总结
红黑树的删除操作就基本介绍完了,总结一下删除操作就是,删除节点等同于删除替换节点,若替换节点是红色节点时,直接删除不会影响平衡;若替换节点是黑色节点时,就需要借用兄弟节点的右子节点、左子节点或者兄弟节点。
红黑树最吸引人的是它的所有操作在最差情况下可以保证 O(logN) 的时间复杂度,稳定且高效。例如要在 10 万条 (2^20) 数据中查找一条数据,只需要 20 次的操作就能完成。但这些保证有一个前置条件,就是数据量不大,且数据可以完全放到内存中。在数据量比较大时,因为红黑树的深度比较大造成磁盘 IO 的频繁读写,会导致它的效率低下。
另外推荐 Data Structure Visualizations 网站,它包含非常多的数据结构方面的可视化算法题。其中就有 红黑树的算法 ,对照着在线生成的红黑树看,会更容易理解红黑树中各种操作场景。
头图:Unsplash
作者:泰阿
原文:https://mp.weixin.qq.com/s/UjZXyISLIp4Ss393O6jOAg
原文:通俗易懂的红黑树图解(下)
来源:政采云前端团队 - 微信公众号 [ID:Zoo-Team]
转载:著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。





